Cara membuat proporsi yang tepat. Cara menghitung proporsi. Cara menyelesaikan masalah menggunakan proporsi
Sederhananya, ini adalah sayuran yang dimasak dalam air sesuai resep khusus. Saya akan mempertimbangkan dua komponen awal (salad sayuran dan air) dan hasil akhirnya - borscht. Secara geometris, ini dapat direpresentasikan sebagai persegi panjang yang satu sisinya melambangkan selada, sisi lainnya melambangkan air. Jumlah kedua sisi ini menunjukkan borscht. Diagonal dan luas persegi panjang "borscht" adalah konsep matematika murni dan tidak pernah digunakan dalam resep borscht.
Bagaimana selada dan air berubah menjadi borscht menurut matematika? Bagaimana cara menjumlahkan dua ruas menjadi trigonometri? Untuk memahami hal ini, kita memerlukan fungsi sudut linier.
Anda tidak akan menemukan apa pun tentang fungsi sudut linier di buku pelajaran matematika. Tapi tanpa mereka tidak akan ada matematika. Hukum matematika, seperti hukum alam, tetap berlaku baik kita mengetahui keberadaannya atau tidak.
Fungsi sudut linier adalah hukum penjumlahan. Lihat bagaimana aljabar berubah menjadi geometri dan geometri berubah menjadi trigonometri.
Apakah mungkin dilakukan tanpa fungsi sudut linier? Anda bisa, karena matematikawan masih dapat melakukannya tanpa mereka. Trik para ahli matematika terletak pada kenyataan bahwa mereka selalu memberi tahu kita hanya tentang masalah-masalah yang dapat mereka pecahkan sendiri, dan tidak pernah memberi tahu kita tentang masalah-masalah yang tidak dapat mereka pecahkan. Melihat. Jika kita mengetahui hasil penjumlahan dan satu suku, kita menggunakan pengurangan untuk mencari suku lainnya. Semua. Kami tidak mengetahui masalah lain dan kami tidak mampu menyelesaikannya. Apa yang harus dilakukan jika kita hanya mengetahui hasil penjumlahan dan tidak mengetahui kedua sukunya? Dalam hal ini, hasil penjumlahan harus didekomposisi menjadi dua suku menggunakan fungsi sudut linier. Selanjutnya, kita sendiri yang memilih salah satu sukunya, dan fungsi sudut linier menunjukkan berapa suku kedua yang seharusnya agar hasil penjumlahannya tepat seperti yang kita butuhkan. Pasangan suku seperti itu jumlahnya tidak terbatas. Dalam kehidupan sehari-hari, kita melakukannya dengan sangat baik tanpa menguraikan jumlahnya; pengurangan sudah cukup bagi kita. Namun dalam studi ilmiah tentang hukum alam, perluasan penjumlahan ke dalam beberapa suku bisa sangat berguna.
Hukum penjumlahan lain yang tidak suka dibicarakan oleh para ahli matematika (trik mereka yang lain) mengharuskan suku-suku tersebut memiliki satuan ukuran yang sama. Untuk selada, air, dan borscht, ini mungkin berupa satuan berat, volume, biaya, atau satuan ukuran.
Gambar tersebut menunjukkan dua tingkat perbedaan dalam matematika. Tingkat pertama adalah perbedaan dalam bidang angka yang ditunjukkan A, B, C. Inilah yang dilakukan para ahli matematika. Tingkat kedua adalah perbedaan luas satuan ukuran, yang ditunjukkan dalam tanda kurung siku dan ditandai dengan huruf kamu. Inilah yang dilakukan fisikawan. Kita dapat memahami tingkat ketiga - perbedaan ruang lingkup objek yang dijelaskan. Benda yang berbeda dapat mempunyai jumlah satuan ukuran yang sama. Betapa pentingnya hal ini dapat kita lihat pada contoh trigonometri borscht. Jika kita menambahkan subskrip ke notasi yang sama untuk satuan pengukuran benda yang berbeda, kita dapat mengetahui dengan tepat besaran matematis apa yang mendeskripsikan suatu benda tertentu dan bagaimana benda itu berubah seiring waktu atau sehubungan dengan tindakan kita. surat W Saya akan menandai air dengan surat itu S Saya akan menandai salad dengan surat itu B- borscht. Berikut tampilan fungsi sudut linier untuk borscht.
Jika kita mengambil sebagian air dan sebagian salad, keduanya akan berubah menjadi satu porsi borscht. Di sini saya sarankan Anda beristirahat sejenak dari borscht dan mengingat masa kecil Anda yang jauh. Ingat bagaimana kita diajari untuk menyatukan kelinci dan bebek? Penting untuk mengetahui berapa banyak hewan yang dihasilkan. Lalu apa yang diajarkan kepada kita untuk dilakukan? Kami diajari untuk memisahkan satuan dari angka dan menjumlahkan angka. Ya, nomor apa pun dapat ditambahkan ke nomor lainnya. Ini adalah jalan langsung menuju autisme matematika modern - kita tidak mengerti apa, tidak jelas mengapa, dan kita sangat kurang memahami bagaimana hal ini berhubungan dengan kenyataan, karena dari tiga tingkat perbedaan, matematikawan hanya beroperasi pada satu tingkat. Akan lebih tepat jika mempelajari cara berpindah dari satu satuan pengukuran ke satuan pengukuran lainnya.
Kelinci, bebek, dan binatang kecil dapat dihitung berkeping-keping. Satu satuan pengukuran umum untuk objek yang berbeda memungkinkan kita untuk menjumlahkannya. Ini adalah masalah versi anak-anak. Mari kita lihat masalah serupa pada orang dewasa. Apa yang Anda dapatkan jika menambahkan kelinci dan uang? Ada dua kemungkinan solusi di sini.
Pilihan pertama. Kami menentukan nilai pasar kelinci dan menambahkannya ke uang tunai yang tersedia. Kami mendapatkan nilai total kekayaan kami dalam bentuk uang.
Pilihan kedua. Anda dapat menambahkan jumlah kelinci ke jumlah uang kertas yang kita miliki. Jumlah harta bergerak akan kita peroleh dalam potongan-potongan.
Seperti yang Anda lihat, hukum penjumlahan yang sama memungkinkan Anda mendapatkan hasil yang berbeda. Itu semua tergantung pada apa sebenarnya yang ingin kita ketahui.
Tapi kembali ke borscht kita. Sekarang kita dapat melihat apa yang akan terjadi pada nilai sudut fungsi sudut linier yang berbeda.
Sudutnya nol. Kami punya salad tapi tidak ada air. Kami tidak bisa memasak borscht. Jumlah borscht juga nol. Ini tidak berarti bahwa nol borscht sama dengan nol air. Zero borsch juga bisa di zero salad (sudut kanan).
Bagi saya pribadi, ini adalah bukti matematis utama dari fakta bahwa . Nol tidak mengubah angka ketika dijumlahkan. Sebab penjumlahan sendiri tidak mungkin dilakukan jika hanya ada satu suku dan suku kedua tidak ada. Anda dapat menghubungkannya dengan ini sesuka Anda, tapi ingat - semua operasi matematika dengan nol ditemukan oleh ahli matematika itu sendiri, jadi buang logika Anda dan dengan bodohnya menjejalkan definisi yang ditemukan oleh ahli matematika: "pembagian dengan nol tidak mungkin", "bilangan apa pun dikalikan dengan nol sama dengan nol", "di belakang titik nol" dan omong kosong lainnya. Cukup diingat sekali bahwa nol bukanlah bilangan, dan Anda tidak akan pernah bertanya-tanya apakah nol itu bilangan asli atau bukan, karena pertanyaan seperti itu umumnya kehilangan makna: bagaimana seseorang dapat menganggap suatu bilangan sebagai bukan bilangan. . Ini seperti menanyakan warna apa untuk mengatribusikan warna yang tidak terlihat. Menambahkan nol pada suatu bilangan ibarat melukis dengan cat yang tidak ada. Mereka melambaikan kuas kering dan memberi tahu semua orang bahwa "kita telah melukis". Tapi saya ngelantur sedikit.
Sudutnya lebih besar dari nol tetapi kurang dari empat puluh lima derajat. Kami punya banyak selada, tapi sedikit air. Hasilnya, kami mendapatkan borscht yang kental.
Sudutnya empat puluh lima derajat. Kami memiliki jumlah air dan selada yang sama. Ini borscht yang sempurna (semoga para juru masak memaafkan saya, ini hanya matematika).
Sudutnya lebih besar dari empat puluh lima derajat tetapi kurang dari sembilan puluh derajat. Kami punya banyak air dan sedikit selada. Dapatkan borscht cair.
Sudut kanan. Kami punya air. Hanya kenangan yang tersisa tentang selada tersebut, saat kami terus mengukur sudut dari garis yang pernah menandai selada tersebut. Kami tidak bisa memasak borscht. Jumlah borscht adalah nol. Kalau begitu, tunggu sebentar dan minum air selagi tersedia)))
Di Sini. Sesuatu seperti ini. Saya dapat menceritakan kisah-kisah lain di sini yang lebih dari pantas di sini.
Kedua sahabat itu mempunyai andil dalam bisnis yang sama. Setelah pembunuhan salah satu dari mereka, semuanya beralih ke yang lain.
Munculnya matematika di planet kita.
Semua cerita ini diceritakan dalam bahasa matematika menggunakan fungsi sudut linier. Di lain waktu saya akan menunjukkan kepada Anda kedudukan sebenarnya dari fungsi-fungsi ini dalam struktur matematika. Sementara itu, mari kembali ke trigonometri borscht dan pertimbangkan proyeksinya.
Sabtu, 26 Oktober 2019
Rabu, 7 Agustus 2019
Mengakhiri pembicaraan tentang , kita perlu mempertimbangkan himpunan tak terhingga. Mengingat bahwa konsep "tak terhingga" berlaku pada ahli matematika, seperti ular boa pada kelinci. Kengerian tak terhingga yang menggetarkan membuat para ahli matematika kehilangan akal sehat. Berikut ini contohnya:
Sumber aslinya berada. Alpha menunjukkan bilangan real. Tanda sama dengan pada ekspresi di atas menunjukkan bahwa jika Anda menambahkan angka atau tak terhingga ke tak terhingga, tidak ada yang berubah, hasilnya akan sama tak terhingga. Jika kita mengambil himpunan bilangan asli tak terhingga sebagai contoh, maka contoh yang dipertimbangkan dapat direpresentasikan sebagai berikut:
Untuk membuktikan kasus mereka secara visual, ahli matematika telah menemukan banyak metode berbeda. Secara pribadi, saya melihat semua metode ini sebagai tarian dukun dengan rebana. Intinya, semuanya bermuara pada kenyataan bahwa beberapa kamar tidak ditempati dan tamu baru ditempatkan di dalamnya, atau beberapa pengunjung dibuang ke koridor untuk memberi ruang bagi para tamu (dengan sangat manusiawi). Saya menyajikan pandangan saya tentang keputusan tersebut dalam bentuk cerita fantastis tentang si Pirang. Berdasarkan apa alasan saya? Memindahkan pengunjung dalam jumlah tak terbatas membutuhkan waktu yang tak terbatas. Setelah kita mengosongkan kamar tamu pertama, salah satu pengunjung akan selalu berjalan menyusuri koridor dari kamarnya ke kamar berikutnya hingga akhir zaman. Tentu saja faktor waktu bisa diabaikan begitu saja, tapi ini sudah termasuk dalam kategori "hukum tidak ditulis untuk orang bodoh". Itu semua tergantung pada apa yang kita lakukan: menyesuaikan kenyataan dengan teori matematika atau sebaliknya.
Apa itu "hotel tanpa batas"? Infinity inn adalah sebuah penginapan yang selalu memiliki jumlah lowongan berapapun, berapa pun jumlah kamar yang ditempati. Jika semua ruangan di lorong tak berujung "untuk pengunjung" terisi, ada lorong tak berujung lainnya dengan ruangan untuk "tamu". Jumlah koridor seperti itu tidak terbatas. Pada saat yang sama, "hotel tanpa batas" memiliki jumlah lantai yang tidak terbatas pada jumlah bangunan yang tidak terbatas pada jumlah planet yang tidak terbatas dalam jumlah alam semesta yang tidak terbatas yang diciptakan oleh Dewa yang jumlahnya tidak terbatas. Sebaliknya, para ahli matematika tidak bisa lepas dari permasalahan sehari-hari yang dangkal: Tuhan-Allah-Buddha selalu hanya satu, hotelnya satu, koridornya hanya satu. Jadi para ahli matematika mencoba menyulap nomor seri kamar hotel, meyakinkan kita bahwa adalah mungkin untuk "mendorong yang tidak didorong".
Saya akan menunjukkan kepada Anda logika alasan saya menggunakan contoh himpunan bilangan asli tak terhingga. Pertama, Anda perlu menjawab pertanyaan yang sangat sederhana: berapa banyak himpunan bilangan asli yang ada - satu atau banyak? Tidak ada jawaban yang benar untuk pertanyaan ini, karena kita sendiri yang menemukan angka, tidak ada angka di Alam. Ya, Alam tahu cara berhitung dengan sempurna, tetapi untuk ini ia menggunakan alat matematika lain yang tidak kita kenal. Seperti yang dipikirkan Alam, saya akan memberitahu Anda lain kali. Sejak kita menemukan bilangan, kita sendiri yang akan memutuskan berapa banyak himpunan bilangan asli yang ada. Pertimbangkan kedua pilihan tersebut, sebagaimana layaknya seorang ilmuwan sejati.
Opsi satu. "Mari kita diberikan" satu set bilangan asli, yang terletak dengan tenang di rak. Kami mengambil set ini dari rak. Itu saja, tidak ada bilangan asli lain yang tersisa di rak dan tidak ada tempat untuk membawanya. Kami tidak dapat menambahkan satu pun ke set ini, karena kami sudah memilikinya. Bagaimana jika Anda benar-benar menginginkannya? Tidak masalah. Kita dapat mengambil satu unit dari set yang telah kita ambil dan mengembalikannya ke rak. Setelah itu, kita dapat mengambil satu unit dari rak dan menambahkannya ke sisa yang ada. Hasilnya, kita kembali mendapatkan himpunan bilangan asli tak terhingga. Anda dapat menulis semua manipulasi kami seperti ini:
Saya telah menuliskan operasi dalam notasi aljabar dan notasi teori himpunan, mencantumkan elemen-elemen himpunan secara rinci. Subskrip menunjukkan bahwa kita mempunyai satu-satunya himpunan bilangan asli. Ternyata himpunan bilangan asli tidak akan berubah hanya jika bilangan tersebut dikurangi satu dan ditambah bilangan yang sama.
Opsi dua. Kita mempunyai banyak himpunan bilangan asli tak terhingga yang berbeda-beda di rak. Saya tekankan - BERBEDA, meskipun faktanya keduanya praktis tidak dapat dibedakan. Kami mengambil salah satu dari set ini. Kemudian kita ambil satu dari himpunan bilangan asli yang lain dan menjumlahkannya ke himpunan yang telah kita ambil. Kita bahkan dapat menjumlahkan dua himpunan bilangan asli. Inilah yang kami dapatkan:
Subskrip "satu" dan "dua" menunjukkan bahwa unsur-unsur ini termasuk dalam himpunan yang berbeda. Ya, kalau dijumlahkan satu ke himpunan tak hingga, hasilnya juga himpunan tak hingga, tapi tidak akan sama dengan himpunan aslinya. Jika himpunan tak hingga lainnya ditambahkan ke satu himpunan tak hingga, hasilnya adalah himpunan tak hingga baru yang terdiri dari elemen-elemen dari dua himpunan pertama.
Himpunan bilangan asli digunakan untuk menghitung dengan cara yang sama seperti penggaris untuk pengukuran. Sekarang bayangkan Anda menambahkan satu sentimeter pada penggaris. Ini akan menjadi garis yang berbeda, tidak sama dengan aslinya.
Anda dapat menerima atau tidak menerima alasan saya - ini urusan Anda sendiri. Namun jika Anda pernah menghadapi masalah matematika, pertimbangkan apakah Anda berada di jalur penalaran yang salah, yang telah dilalui oleh generasi ahli matematika. Bagaimanapun, kelas matematika, pertama-tama, membentuk stereotip berpikir yang stabil dalam diri kita, dan baru kemudian menambah kemampuan mental kita (atau sebaliknya, menghilangkan kebebasan berpikir kita).
pozg.ru
Minggu, 4 Agustus 2019
Saya sedang menulis catatan tambahan untuk sebuah artikel tentang dan melihat teks indah ini di Wikipedia:
Kita membaca: "... landasan teori yang kaya dari matematika Babel tidak memiliki karakter holistik dan direduksi menjadi seperangkat teknik yang berbeda, tanpa sistem dan basis bukti yang sama."
Wow! Seberapa pintar kita dan seberapa baik kita bisa melihat kekurangan orang lain. Apakah lemah bagi kita untuk melihat matematika modern dalam konteks yang sama? Sedikit memparafrasekan teks di atas, secara pribadi saya mendapatkan yang berikut:
Landasan teori matematika modern yang kaya tidak bersifat holistik dan direduksi menjadi sekumpulan bagian-bagian yang berbeda, tanpa sistem umum dan basis bukti.
Saya tidak akan pergi jauh untuk mengkonfirmasi kata-kata saya - ia memiliki bahasa dan konvensi yang berbeda dari bahasa dan konvensi banyak cabang matematika lainnya. Nama yang sama pada cabang matematika yang berbeda dapat mempunyai arti yang berbeda. Saya ingin mengabdikan seluruh siklus publikasi untuk kesalahan paling nyata dalam matematika modern. Sampai berjumpa lagi.
Sabtu, 3 Agustus 2019
Bagaimana cara membagi suatu himpunan menjadi himpunan bagian? Untuk melakukan ini, Anda harus memasukkan satuan ukuran baru, yang ada di beberapa elemen himpunan yang dipilih. Perhatikan sebuah contoh.
Semoga kita punya banyak A terdiri dari empat orang. Himpunan ini dibentuk atas dasar “orang”. Mari kita tentukan unsur-unsur himpunan ini melalui huruf A, subskrip dengan nomor akan menunjukkan nomor urut setiap orang dalam himpunan ini. Mari kita perkenalkan satuan pengukuran baru "karakteristik seksual" dan nyatakan dengan huruf B. Karena karakteristik seksual melekat pada semua orang, kami mengalikan setiap elemen dari himpunan tersebut A tentang gender B. Perhatikan bahwa kumpulan "orang" kita kini telah menjadi kumpulan "orang dengan gender". Setelah itu, kita bisa membagi ciri-ciri seksual menjadi laki-laki bm dan wanita bw karakteristik gender. Sekarang kita dapat menerapkan filter matematis: kita memilih salah satu dari ciri-ciri seksual ini, tidak peduli yang mana laki-laki atau perempuan. Kalau ada pada seseorang, maka kita kalikan dengan satu, jika tidak ada tandanya, kita kalikan dengan nol. Dan kemudian kami menerapkan matematika sekolah biasa. Lihat apa yang terjadi.
Setelah perkalian, reduksi, dan penataan ulang, kita mendapatkan dua himpunan bagian: himpunan bagian laki-laki bm dan sebagian perempuan bw. Kira-kira dengan cara yang sama para ahli matematika bernalar ketika mereka menerapkan teori himpunan dalam praktik. Namun mereka tidak memberi tahu kita rinciannya, namun memberi kita hasil akhirnya - "banyak orang terdiri dari sebagian laki-laki dan sebagian perempuan." Tentu saja, Anda mungkin memiliki pertanyaan, bagaimana cara menerapkan matematika dengan benar dalam transformasi di atas? Saya berani meyakinkan Anda bahwa sebenarnya transformasi dilakukan dengan benar, cukup mengetahui pembenaran matematis aritmatika, aljabar Boolean, dan bagian matematika lainnya. Apa itu? Lain kali saya akan menceritakannya kepada Anda.
Sedangkan untuk superset, dua himpunan dapat digabungkan menjadi satu superset dengan memilih satuan ukuran yang ada pada elemen kedua himpunan tersebut.
Seperti yang Anda lihat, satuan pengukuran dan matematika umum menjadikan teori himpunan ketinggalan jaman. Tanda bahwa teori himpunan tidak berjalan baik adalah para ahli matematika telah menciptakan bahasa dan notasi mereka sendiri untuk teori himpunan. Para ahli matematika melakukan apa yang dulu dilakukan para dukun. Hanya dukun yang tahu bagaimana menerapkan "pengetahuan" mereka dengan "benar". "Pengetahuan" ini mereka ajarkan kepada kita.
Terakhir, saya ingin menunjukkan kepada Anda bagaimana matematikawan memanipulasi.
Senin, 7 Januari 2019
Pada abad kelima SM, filsuf Yunani kuno Zeno dari Elea merumuskan aporiasnya yang terkenal, yang paling terkenal adalah aporia "Achilles dan kura-kura". Begini bunyinya:
Katakanlah Achilles berlari sepuluh kali lebih cepat dari kura-kura dan berada seribu langkah di belakangnya. Selama Achilles berlari sejauh ini, kura-kura merangkak seratus langkah ke arah yang sama. Ketika Achilles sudah berlari seratus langkah, kura-kura akan merangkak sepuluh langkah lagi, dan seterusnya. Prosesnya akan terus berlanjut tanpa batas waktu, Achilles tidak akan pernah bisa mengejar kura-kura.
Alasan ini menjadi kejutan logis bagi semua generasi berikutnya. Aristoteles, Diogenes, Kant, Hegel, Gilbert... Semuanya, dengan satu atau lain cara, dianggap sebagai aporia Zeno. Guncangannya begitu kuat sehingga " ... diskusi berlanjut hingga saat ini, komunitas ilmiah belum berhasil mencapai konsensus tentang esensi paradoks ... analisis matematis, teori himpunan, pendekatan fisik dan filosofis baru dilibatkan dalam studi masalah ini ; tidak satupun dari mereka menjadi solusi yang diterima secara universal untuk masalah ini ..."[Wikipedia," Zeno's Aporias "]. Semua orang mengerti bahwa mereka sedang dibodohi, tapi tidak ada yang mengerti apa penipuan itu.
Dari sudut pandang matematika, Zeno dalam aporianya dengan jelas menunjukkan transisi dari nilai ke. Transisi ini menyiratkan penerapan alih-alih konstanta. Sejauh yang saya pahami, peralatan matematika untuk menerapkan satuan pengukuran variabel belum dikembangkan, atau belum diterapkan pada aporia Zeno. Penerapan logika yang biasa kita lakukan membawa kita ke dalam perangkap. Kita, karena kelembaman berpikir, menerapkan satuan waktu yang konstan pada kebalikannya. Dari sudut pandang fisik, sepertinya waktu melambat hingga berhenti total pada saat Achilles mengejar kura-kura. Jika waktu berhenti, Achilles tidak bisa lagi menyusul kura-kura tersebut.
Jika kita mengubah logika yang biasa kita gunakan, semuanya akan beres. Achilles berlari dengan kecepatan konstan. Setiap segmen jalur berikutnya sepuluh kali lebih pendek dari segmen sebelumnya. Oleh karena itu, waktu yang dibutuhkan untuk mengatasinya sepuluh kali lebih sedikit dibandingkan waktu sebelumnya. Jika kita menerapkan konsep "tak terhingga" dalam situasi ini, maka benar jika dikatakan "Achilles akan segera menyusul kura-kura."
Bagaimana cara menghindari jebakan logis ini? Tetap dalam satuan waktu yang konstan dan jangan beralih ke nilai timbal balik. Dalam bahasa Zeno, tampilannya seperti ini:
Dalam waktu yang dibutuhkan Achilles untuk berlari seribu langkah, kura-kura merangkak seratus langkah ke arah yang sama. Selama selang waktu berikutnya, sama dengan yang pertama, Achilles akan berlari seribu langkah lagi, dan kura-kura akan merangkak seratus langkah. Kini Achilles berada delapan ratus langkah di depan kura-kura.
Pendekatan ini cukup menggambarkan realitas tanpa adanya paradoks logis. Tapi ini bukanlah solusi lengkap untuk masalah ini. Pernyataan Einstein tentang kecepatan cahaya yang tidak dapat diatasi sangat mirip dengan aporia Zeno "Achilles dan kura-kura". Kami belum mempelajari, memikirkan kembali, dan memecahkan masalah ini. Dan solusinya harus dicari bukan dalam jumlah yang sangat besar, namun dalam satuan pengukuran.
Aporia menarik lainnya dari Zeno menceritakan tentang panah terbang:
Anak panah yang terbang tidak bergerak, karena ia diam pada setiap saat, dan karena ia diam pada setiap saat, maka ia selalu diam.
Dalam aporia ini, paradoks logis diatasi dengan sangat sederhana - cukup untuk memperjelas bahwa pada setiap momen waktu panah terbang berhenti di berbagai titik di ruang angkasa, yang sebenarnya adalah gerakan. Ada hal lain yang perlu diperhatikan di sini. Dari satu foto sebuah mobil di jalan raya, tidak mungkin untuk menentukan fakta pergerakannya atau jaraknya. Untuk menentukan fakta pergerakan mobil, diperlukan dua buah foto yang diambil dari titik yang sama pada titik waktu yang berbeda, tetapi tidak dapat digunakan untuk menentukan jarak. Untuk menentukan jarak ke mobil, Anda memerlukan dua foto yang diambil dari titik berbeda di ruang angkasa pada saat yang sama, tetapi Anda tidak dapat menentukan fakta pergerakan dari foto tersebut (tentu saja, Anda masih memerlukan data tambahan untuk perhitungan, trigonometri akan membantu Anda). Yang ingin saya tekankan secara khusus adalah bahwa dua titik dalam waktu dan dua titik dalam ruang adalah dua hal berbeda yang tidak boleh dikacaukan karena keduanya memberikan peluang eksplorasi yang berbeda.
Saya akan menunjukkan prosesnya dengan sebuah contoh. Kami memilih "merah padat dalam jerawat" - ini adalah "keseluruhan" kami. Pada saat yang sama, kita melihat bahwa benda-benda ini ada yang memiliki busur, dan ada yang tidak memiliki busur. Setelah itu, kita pilih bagian dari "keseluruhan" dan membentuk satu set "dengan busur". Beginilah cara para dukun memberi makan diri mereka sendiri dengan mengaitkan teori himpunan mereka dengan kenyataan.
Sekarang mari kita lakukan sedikit trik. Mari kita ambil "padat dalam jerawat dengan busur" dan satukan "keseluruhan" ini berdasarkan warna, pilih elemen merah. Kami mendapat banyak "merah". Sekarang pertanyaan rumitnya: apakah himpunan yang diterima "dengan busur" dan "merah" adalah himpunan yang sama atau dua himpunan berbeda? Hanya dukun yang tahu jawabannya. Lebih tepatnya, mereka sendiri tidak tahu apa-apa, tapi seperti kata mereka, biarlah.
Contoh sederhana ini menunjukkan bahwa teori himpunan sama sekali tidak berguna jika dikaitkan dengan kenyataan. Apa rahasianya? Kami membentuk satu set "jerawat merah padat dengan busur". Pembentukannya terjadi menurut empat satuan pengukuran yang berbeda: warna (merah), kekuatan (padat), kekasaran (dalam bentuk benjolan), dekorasi (dengan busur). Hanya seperangkat satuan pengukuran yang memungkinkan untuk mendeskripsikan objek nyata secara memadai dalam bahasa matematika. Berikut tampilannya.
Huruf "a" dengan indeks berbeda menunjukkan satuan pengukuran yang berbeda. Dalam tanda kurung, satuan pengukuran disorot, yang menurutnya "keseluruhan" dialokasikan pada tahap awal. Satuan ukuran yang menjadi dasar pembentukan himpunan tersebut dikeluarkan dari tanda kurung. Baris terakhir menunjukkan hasil akhir - elemen himpunan. Seperti yang Anda lihat, jika kita menggunakan satuan untuk membentuk suatu himpunan, maka hasilnya tidak bergantung pada urutan tindakan kita. Dan ini matematika, dan bukan tarian dukun dengan rebana. Dukun dapat “secara intuitif” sampai pada hasil yang sama, memperdebatkannya dengan “kejelasan”, karena satuan pengukuran tidak termasuk dalam persenjataan “ilmiah” mereka.
Dengan menggunakan satuan ukuran, sangat mudah untuk memecah satu atau menggabungkan beberapa himpunan menjadi satu superset. Mari kita lihat lebih dekat aljabar dari proses ini.
Ingat!
Dengan tiga anggota proporsi yang diketahui, Anda selalu dapat menemukan anggota (keempat) yang tidak diketahui.
memecahkan proporsi berarti menemukan semua anggotanya. Mari kita selesaikan proporsinya di bawah ini
(temukan "x").

Untuk mencari " x", Kami menggunakan properti utama proporsi (aturan "silang").
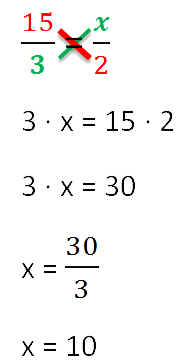
Sekarang kita siap mencari cara untuk menyelesaikan soal proporsi.
Memecahkan masalah proporsi
Sering tugas proporsi berkaitan erat dengan persentase. Anda dapat memoles pengetahuan Anda tentang persentase di bagian "Minat".
Tugas
50 tembakan dilepaskan dari haluan. 5 anak panah terbang melewati sasaran. Tentukan persentase pukulan.
Secara tradisi, kami menekankan data penting dan numerik dalam soal.
Perhatikan bahwa kita perlu menentukan persentase kena, bukan persentase anak panah yang meleset.
Oleh karena itu, kita hitung dulu berapa banyak anak panah yang mengenai sasaran. Ini tidak akan sulit untuk dilakukan.
- 50 − 5 = 45 (panah) - mencapai target.
Selanjutnya untuk mengatasi masalah tersebut, kita akan membuat tabel dimana kita akan memasukkan semua datanya. Ingatlah bahwa di seberang 100% dalam tabel biasanya tertulis jumlah total sesuatu. Persentase yang tidak diketahui akan dilambangkan dengan huruf x.
Untuk mencatat data yang diperlukan dalam tabel dengan benar, ingatlah aturan sederhana.
Persamaan dua perbandingan disebut proporsi.
a :b =c :d. Ini adalah proporsi. Membaca: A jadi berlaku untuk B, Bagaimana C mengacu pada D. Angka A Dan D ditelepon ekstrim anggota proporsi, dan angka B Dan C – rata-rata anggota proporsi.
Contoh Proporsi: 1 2 : 3 = 16 : 4 . Inilah persamaan dua perbandingan: 12:3= 4 dan 16:4= 4 . Bunyinya: dua belas berbanding tiga, enam belas berbanding empat. Di sini 12 dan 4 adalah anggota ekstrim dari proporsi tersebut, dan 3 dan 16 adalah anggota tengah dari proporsi tersebut.
Properti dasar proporsi.
Hasil kali suku ekstrim suatu proporsi sama dengan hasil kali suku tengahnya.
Untuk proporsi a :b =c :d atau a/b=c/d properti utama ditulis seperti ini: sebuah d \u003d b c .
Untuk perbandingan kita 12 : 3 = 16 : 4 sifat utamanya akan ditulis sebagai berikut: 12 4 = 3 16 . Ternyata persamaan yang benar: 48 = 48 .
Untuk mencari suku ekstrem suatu proporsi yang belum diketahui, Anda perlu membagi hasil kali suku rata-rata suatu proporsi dengan suku ekstrem yang diketahui.
Contoh.
1) x: 20 = 2: 5. Kita punya X Dan 5 adalah anggota ekstrim dari proporsi, dan 20 Dan 2 - sedang.
Larutan.
x = (20 2):5- Anda perlu mengalikan suku tengahnya ( 20 Dan 2 ) dan membagi hasilnya dengan suku ekstrim yang diketahui (angka 5 );
x=40:5 adalah hasil kali suku tengah ( 40 ) dibagi dengan suku ekstrem yang diketahui ( 5 );
x = 8. Kami mendapatkan suku ekstrim proporsi yang diinginkan.
Lebih mudah untuk menuliskan penemuan anggota proporsi yang tidak diketahui menggunakan pecahan biasa. Berikut adalah bagaimana contoh yang telah kita pertimbangkan akan ditulis:
Suku ekstrim yang diinginkan dari proporsi ( X) akan sama dengan hasil kali suku tengah ( 20 Dan 2 ) dibagi dengan suku ekstrim yang diketahui ( 5 ).
Kami mengurangi pecahan sebesar 5 (dibagi dengan 5 X.
Lebih banyak contoh menemukan anggota ekstrim proporsi yang tidak diketahui.

Untuk mencari suku tengah suatu proporsi yang belum diketahui, Anda perlu membagi hasil kali suku ekstrem suatu proporsi dengan suku tengah yang diketahui.
Contoh. Temukan suku tengah proporsi yang tidak diketahui.
5) 9:x = 3:14. Nomor 3 adalah suku rata-rata yang diketahui dari proporsi tertentu, angka 9 Dan 14 adalah syarat ekstrim dari proporsi tersebut.
Larutan.
x = (9 14): 3 - mengalikan suku ekstrim dari proporsi tersebut dan membagi hasilnya dengan suku tengah proporsi yang diketahui;
x= 136:3;
x=42.
Solusi untuk contoh ini dapat ditulis secara berbeda:
 Suku rata-rata yang diperlukan dari proporsi ( X) akan sama dengan hasil kali suku ekstrim ( 9
Dan 14
) dibagi dengan suku tengah yang diketahui ( 3
).
Suku rata-rata yang diperlukan dari proporsi ( X) akan sama dengan hasil kali suku ekstrim ( 9
Dan 14
) dibagi dengan suku tengah yang diketahui ( 3
).
Kami mengurangi pecahan sebesar 3 (dibagi dengan 3 dan pembilang dan penyebut pecahan). Menemukan nilainya X.
Jika Anda lupa cara mereduksi pecahan biasa, ulangi topik: ""
Lebih banyak contoh tentang menemukan anggota rata-rata proporsi yang tidak diketahui.

Bagian: Matematika
Jenis pelajaran: Pelajaran belajar dan konsolidasi utama pengetahuan baru.
Bentuk pelajaran: Pelajaran-penelitian.
Tujuan Pelajaran:
- untuk mengaktifkan aktivitas kognitif siswa;
- mengenalkan siswa pada konsep: proporsi, anggota proporsi; proporsi yang benar dan salah;
- mengenalkan siswa pada sifat dasar perbandingan dan membentuk keterampilan menentukan perbandingan yang benar.
Peralatan:
Lembar rute menunjukkan titik-titik yang dapat diperoleh untuk menyelesaikan tugas. Saat menilai, siswa memperhitungkan kebenaran keputusannya, kecepatan pengambilan keputusan (self-check dan mutual check dengan bantuan presentasi). Pada baris “Poin tambahan”, poin diberikan untuk menjawab pertanyaan tambahan, untuk membantu guru mengatur pengujian siswa lain, dan juga untuk “menebak” topik pelajaran.
Kartu dipotong dan dibagikan dalam amplop kepada siswa (satu amplop per meja).
3. Kartu untuk papan magnet (Gambar 1, Gambar 2, Gambar 3)
Selama pembelajaran, kartu-kartu ini ditempel di papan magnet.
4. Puzzle (Gambar 4, Gambar 5, Gambar 6, Gambar 7).




Rebus yang disusun oleh siswa SMA (kecuali rebus “Proporsi” - rebus ini diambil dari pelajaran yang disampaikan di FPI oleh guru Kozak Tatyana Ivanovna, Sekolah Menengah No. 20 Kemajuan, Wilayah Amur) terletak di papan tulis, siswa berada diundang untuk menyelesaikannya setelah pelajaran.
Peralatan teknis pembelajaran adalah komputer, proyektor untuk memperagakan presentasi, layar. Presentasi komputer di Microsoft PowerPoint (Lampiran 4).
I. Organisasi awal pelajaran
Halo! Harap periksa apakah Anda memiliki handout di meja Anda, apakah Anda memiliki pensil merah dan biru, dan apakah Anda siap untuk pelajaran.
II. Pesan topik, maksud dan tujuan pelajaran.
Hari ini dalam pelajaran kita terus mempelajari sebagian besar mata pelajaran matematika. Kami telah selesai mempelajari topik (apa? - "Sikap"). Sekarang kami mulai mengeksplorasi topik baru di bagian ini. Beberapa contoh akan membantu kita memahami topik pelajaran. Pada halaman judul lembar rute Anda, Anda perlu mengisi tabel dengan menyelesaikan contoh secara lisan dan kemudian Anda akan mengetahui topik pelajaran hari ini. GESER 1
Jadi, topik pelajaran hari ini Proporsi. GESER 2
Mengetahui topik pelajaran, cobalah membuat rencana pembelajaran. Apa yang harus Anda pelajari di kelas hari ini? Apa yang ingin kamu ketahui? Apa yang ingin kamu pelajari di kelas?
Kami akan membuat rencana, yang akan kami tambahkan selama pelajaran. (siswa menyebutkan dua poin pertama dan dua poin terakhir dari rencana, sisanya diisi selama pembelajaran, karena pengetahuan baru “ditemukan”; rencana pembelajaran ditulis di papan tulis)
- pengulangan (pertanyaan yang berhubungan dengan sikap)
Definisi proporsi
ANGGOTA PROPORSI
PROPORSI YANG BENAR DAN SALAH
SIFAT UTAMA PROPORSI
Penerapan dalam matematika
Penerapan dalam kehidupan
Kita akan dapat menganalisis dua poin terakhir dalam pelajaran berikut, saat kita mempelajari topik tersebut.
AKU AKU AKU. Memperbarui pengetahuan siswa. Persiapan aktivitas pendidikan dan kognitif aktif pada tahap utama pembelajaran.
Diskusikan pertanyaan-pertanyaan yang berkaitan dengan topik “Sikap” dengan teman sekelas.
Siapa yang siap bertanya terkait topik terakhir? (badai salju) MP1
- Apa itu sikap?
Bagaimana Anda bisa menulis suatu hubungan?
Pertanyaan apa yang dijawab oleh sikap?
Bagaimana cara menulis perbandingan dua bilangan?
Apa yang bisa menggantikan tanda do?
Menurut Anda mengapa kami mengulangi konsep ini?
Mereka akan membantu kita ketika mempelajari topik baru.
Ambil amplopnya dan perbaiki hubungan A Ke B Dan C Ke D dua arah. (hanya 4 relasi) BEKERJA BERPASANG.
MP2 Anda memiliki beberapa hubungan di depan Anda. Temukan arti dari ungkapan-ungkapan ini. GESER 3
4: 0,5= = 5: 10 = = 8: 1 = 2,5: 5 =
Kelompokkan hubungan-hubungan tersebut menurut atribut tertentu dan buatlah persamaan-persamaan yang sesuai.
IV. Asimilasi pengetahuan baru.
4: 0,5 = 8: 1 = 5: 10 = 2,5: 5
Atas dasar apa Anda mengelompokkan hubungan-hubungan ini?
- Nilai-nilai mereka setara.
Persamaan yang dihasilkan disebut proporsi.
Pikirkan dan tentukan proporsi.
PETUNJUK - proporsinya adalah ... DI LAYAR ( persamaan)
Kesetaraan…APA ( hubungan)
Berapa banyak hubungan? ( dua).
Siapa yang yakin dengan pendapatnya, tuliskan definisinya di lembar rute. MP3
Siapa yang siap pergi ke papan tulis dan menyusun definisi proporsi? (Lampiran 3)
DEFINISI (pada papan magnet): Proporsi adalah persamaan dua rasio.
Mari kita lihat interpretasi kata proporsi dalam kamus bahasa Rusia Ozhegov S.I. GESER 4: “Proporsi adalah perbandingan tertentu antara bagian-bagian satu sama lain, proporsionalitas. Dalam matematika, persamaan dua rasio.Anda telah merumuskan definisi proporsi dengan cara yang sama seperti dalam kamus bahasa Rusia!
Pikirkan tentang istilah matematika apa yang sesuai dengan kata "proporsi"? ( minat). Bagaimana istilah "persentase" diterjemahkan? ( dari seratus). Jadi, "pro" diterjemahkan sebagai "dari". Bagian kata mana yang tersisa? (“ sebagian”). Di mana Anda menemukan kata ini? (dalam memasak) Apa artinya? ( ukuran)
Kata proporsi berasal dari kata latin proportio – proporsionalitas. (kamus etimologis). GESER 4
Dengan menggunakan definisi perbandingan, tulislah perbandingan dengan menggunakan tanda pembagian dan garis pecahan. (BEKERJA BERPASANG, amplop).
Pada lembar rute, tuliskan proporsinya dengan menggunakan huruf a, b, c, d. MP4
Dan sekarang kita akan mengetahui apa nama bilangan-bilangan yang menyusun proporsi tersebut.
Angka a, b, c, d disebut anggota proporsi
Berapakah suku pertama dan suku terakhir suatu perbandingan? ( a dan c)
Dan apa yang biasanya (dalam hidup) disebut yang pertama dan terakhir? (ekstrim)
Jadi suku a dan b disebut...? (ekstrim)
Dimana suku c dan d? (di tengah-tengah)
Dan siapa nama anggota c dan d? ( sedang)
Anggota mana yang disorot dengan warna merah? ( Ke lebih awal)
warna (Dengan langka) anggota.anggota tengah

Mari kita kembali ke rencana pelajaran - apakah Anda memiliki sesuatu untuk ditambahkan ke dalamnya? (anggota proporsi ekstrem dan tengah)
V. Konsolidasi pengetahuan primer
MP5 Isi tabelnya:
Kesimpulan apa yang bisa diambil? Catat hasilnya pada rencana perjalanan. ( Secara proporsional, hasil kali suku ekstrim sama dengan hasil kali suku tengah)GESER 8
MP6 Berikut adalah lima persamaan. Apakah semuanya proporsional?
Tekankan proporsi.
= ; 7 + 11 = 36: 2; 72: 9 = 16: 2; = 20: 4; 5 40 = 100 2SLIDE 7 Berdiri, siapa yang sudah selesai.
Apakah semua orang yakin ada tiga proporsi di sini? Memang, pada persamaan terakhir, hasil kali suku-suku ekstrim tidak sama dengan hasil kali suku-suku tengah. Mari kita kembali ke definisi proporsi ( Proporsi - persamaan dua rasio). Apakah persamaan ketiga merupakan persamaan kedua relasi? (adalah). Menurut definisinya, apakah ini sebuah proporsi? (Ya). Apakah hasil kali suku ekstrim sama dengan hasil kali suku tengah? (TIDAK). Jadi itu proporsinya...? (salah). Proporsi ini disebut salah. Jadi, ada proporsi yang salah dan...? (setia). Merumuskan sifat dasar proporsi, dengan menggunakan pengetahuan yang diperoleh. (Dalam perbandingan yang tepat, hasil kali suku-suku ekstrim sama dengan hasil kali suku-suku tengah).
VI. Konsolidasi pengetahuan.
Isi tabelnya.
Proporsi yang benar Proporsi yang salah
= = 20: 4
Bagaimana lagi Anda bisa menentukan proporsi yang benar atau salah? (temukan nilai hubungannya)
Di masa depan, kita akan membicarakan proporsi yang benar.
Mari kita kembali ke rencana pelajaran. Apa yang bisa ditambahkan? (proporsi benar dan salah)
MP7 Dengan menggunakan huruf B dan H, tandai proporsi yang benar dan salah.
= 1: 0,5 = 4,8: 2,4 7,5: 5 = 2: 3 = 10: 3 = 3 : 1 5:x = 20:4x
VII. Generalisasi dan sistematisasi.
MP8 Dengan menggunakan sifat dasar proporsi, buatlah proporsi yang benar dari bilangan berikut: 4, 5, 12, 15. Berapa banyak proporsi benar yang dapat kamu buat?
VIII. Kontrol dan uji diri pengetahuan
Dikte Matematika MP9
- Tuliskan perbandingannya: Angka 18 berhubungan dengan 4 sebagaimana 27 berhubungan dengan 6.
- Tuliskan perbandingannya: Perbandingan tiga banding lima sama dengan perbandingan dua banding tujuh.
- Tuliskan rata-rata suku perbandingannya: 1,5:2 = 4,5:6
- Tuliskan anggota ekstrim dari perbandingan tersebut: 2/1.9 = 3/2.8
- Apakah proporsi pada angka 3 sudah benar?
- Apakah proporsi pada angka 4 sudah benar?
- Apakah pernyataan tersebut benar: Akar persamaannya adalah 20/5 = x / 0,5 bilangan 2
- Apakah pernyataan berikut ini benar: Empat bilangan asli mana pun dapat digunakan untuk membentuk proporsi?
SLIDE 10. Tinjauan sejawat
IX. Menyimpulkan pelajaran.
Silakan merujuk pada rencana pelajaran.
Apa yang kamu pelajari di kelas hari ini? (apa itu proporsi, terdiri dari apa proporsi, proporsi yang benar dan salah, sifat utama dari suatu proporsi, ...)
Apa yang kamu pelajari di kelas hari ini? (tentukan anggota ekstrim dan tengah dari proporsi tersebut, cari tahu apakah proporsi tersebut benar atau salah, ...)
Pertanyaan lain apa yang bisa ditanyakan di akhir pelajaran?
-Berapa banyak perbandingan tepat yang dapat dibuat dari perbandingan tepat tersebut?
Bagaimana cara mengetahui suatu proporsi benar atau salah?
Mari kita ingat tugas terakhir dari dikte matematika.
Empat bilangan asli apa pun dapat digunakan untuk membentuk proporsi. Jawaban yang benar adalah YA. Anda dapat membuat proporsinya, tetapi itu belum tentu benar.
Dari kalimat “ Empat bilangan asli apa pun dapat digunakan untuk membentuk proporsi. Hilangkan satu kata untuk membuat pernyataan ini salah. (alami). Mengapa? (Angka 0 tidak dapat menjadi anggota suatu proporsi). Empat angka apa pun dapat digunakan untuk membentuk proporsi
Dalam frasa ini Empat bilangan asli apa pun dapat digunakan untuk membentuk proporsi. masukkan satu kata untuk membuat pernyataan itu salah (BENAR). Dari empat bilangan asli mana pun, Anda dapat membuat proporsi yang benar.
Hitung jumlah poin yang Anda peroleh dalam pelajaran dan berikan nilai.
X. Informasi tentang pekerjaan rumah dan petunjuk cara menyelesaikannya
Matematika - 6, Vilenkin N.Ya. dkk.edisi ke-6
Hlm.21, No.760, 781, 782, 783 (a)
Perbandingan dua bilangan
Definisi 1
Perbandingan dua bilangan adalah privasi mereka.
Contoh 1
perbandingan $18$ dengan $3$ dapat ditulis sebagai:
$18\div 3=\frac(18)(3)=6$.
perbandingan $5$ dengan $15$ dapat ditulis sebagai:
$5\div 15=\frac(5)(15)=\frac(1)(3)$.
Dengan menggunakan perbandingan dua bilangan dapat ditampilkan:
- berapa kali suatu angka lebih besar dari angka lainnya;
- bagian apa yang diwakili oleh satu angka dari angka lainnya.
Saat membuat perbandingan dua bilangan pada penyebut suatu pecahan, tuliskan bilangan yang digunakan untuk membandingkannya.
Paling sering, angka seperti itu mengikuti kata "dibandingkan dengan ..." atau kata depan "ke ...".
Ingat kembali sifat dasar pecahan dan terapkan pada suatu relasi:
Catatan 1
Saat mengalikan atau membagi kedua suku relasi dengan bilangan yang sama selain nol, kita memperoleh perbandingan yang sama dengan bilangan aslinya.
Perhatikan contoh yang mengilustrasikan penggunaan konsep perbandingan dua bilangan.
Contoh 2
Jumlah curah hujan pada bulan sebelumnya adalah $195$ mm, dan pada bulan ini - $780$ mm. Berapa peningkatan jumlah curah hujan pada bulan ini dibandingkan bulan sebelumnya?
Larutan.
Tulislah perbandingan jumlah curah hujan pada bulan berjalan dengan jumlah curah hujan pada bulan sebelumnya:
$\frac(780)(195)=\frac(780\div 5)(195\div 5)=\frac(156\div 3)(39\div 3)=\frac(52)(13)=4 $.
Menjawab: jumlah curah hujan pada bulan ini adalah $4$ kali lebih banyak dibandingkan bulan sebelumnya.
Contoh 3
Tentukan berapa kali bilangan $1 \frac(1)(2)$ terdapat dalam bilangan $13 \frac(1)(2)$.
Larutan.
$13 \frac(1)(2)\div 1 \frac(1)(2)=\frac(27)(2)\div \frac(3)(2)=\frac(27)(2) \cdot \frac(2)(3)=\frac(27)(3)=9$.
Menjawab: $9$ kali.
Konsep proporsi
Definisi 2
Proporsi disebut persamaan dua relasi:
$a\div b=c\div d$
$\frac(a)(b)=\frac(c)(d)$.
Contoh 4
$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,
$\frac(8)(2)=\frac(36)(9)$, $\frac(10)(40)=\frac(9)(36)$, $\frac(15)(75)= \frac(1)(5)$.
Pada perbandingan $\frac(a)(b)=\frac(c)(d)$ (atau $a:b = c\div d$), bilangan a dan d disebut anggota ekstrim proporsi, sedangkan angka $b$ dan $c$ adalah anggota tengah proporsi.
Proporsi yang benar dapat diubah sebagai berikut:
Catatan 2
Hasil kali suku-suku ekstrim dari perbandingan yang benar sama dengan hasil kali suku-suku tengah:
$a \cdot d=b \cdot c$.
Pernyataan ini adalah sifat dasar proporsi.
Kebalikannya juga benar:
Catatan 3
Jika hasil kali suku ekstrim suatu proporsi sama dengan hasil kali suku tengahnya, maka proporsi tersebut benar.
Catatan 4
Apabila suku-suku tengah atau suku-suku ekstrim disusun kembali dengan perbandingan yang benar, maka perbandingan yang diperoleh juga akan benar.
Contoh 5
$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,
$\frac(2)(8)=\frac(9)(36)$, $\frac(40)(10)=\frac(36)(9)$, $\frac(75)(15)= \frac(5)(1)$.
Dengan menggunakan sifat ini, mudah untuk menemukan suku yang tidak diketahui dari suatu proporsi jika tiga suku lainnya diketahui:
$a=\frac(b \cdot c)(d)$; $b=\frac(a \cdot d)(c)$; $c=\frac(a \cdot d)(b)$; $d=\frac(b \cdot c)(a)$.
Contoh 6
$\frac(6)(a)=\frac(16)(8)$;
$6 \cdot 8=16 \cdot a$;
$16 \cdot a=6 \cdot 8$;
$16 \cdot a=48$;
$a=\frac(48)(16)$;
Contoh 7
$\frac(a)(21)=\frac(8)(24)$;
$a \cdot 24=21 \cdot 8$;
$a \cdot 24=168$;
$a=\frac(168)(24)$;
$3 tukang kebun - $108 pohon;
$x$ tukang kebun - $252$ pohon.
Mari kita buat proporsinya:
$\frac(3)(x)=\frac(108)(252)$.
Mari kita gunakan aturan untuk mencari suku proporsi yang tidak diketahui:
$b=\frac(a \cdot d)(c)$;
$x=\frac(3 \cdot 252)(108)$;
$x=\frac(252)(36)$;
Menjawab: Dibutuhkan $7$ tukang kebun untuk memangkas $252$ pohon.
Paling sering, sifat-sifat proporsi digunakan dalam praktik dalam perhitungan matematis dalam kasus di mana perlu untuk menghitung nilai anggota proporsi yang tidak diketahui, jika nilai dari tiga anggota lainnya diketahui.
