Come fare la giusta proporzione. Come calcolare la proporzione. Come risolvere un problema utilizzando la proporzione

In poche parole, si tratta di verdure cotte in acqua secondo una ricetta speciale. Considererò due componenti iniziali (insalata di verdure e acqua) e il risultato finale: il borscht. Dal punto di vista geometrico, questo può essere rappresentato come un rettangolo in cui un lato indica la lattuga, l'altro lato indica l'acqua. La somma di questi due lati denoterà il borscht. La diagonale e l'area di un rettangolo di questo tipo "borscht" sono concetti puramente matematici e non vengono mai utilizzate nelle ricette del borscht.

In che modo la lattuga e l'acqua si trasformano in borscht in termini matematici? Come può la somma di due segmenti trasformarsi in trigonometria? Per capirlo, abbiamo bisogno delle funzioni angolari lineari.

Non troverai nulla sulle funzioni degli angoli lineari nei libri di testo di matematica. Ma senza di essi non può esserci matematica. Le leggi della matematica, come le leggi della natura, funzionano sia che sappiamo che esistono oppure no.

Le funzioni angolari lineari sono le leggi dell'addizione. Guarda come l'algebra si trasforma in geometria e la geometria si trasforma in trigonometria.

È possibile fare a meno delle funzioni angolari lineari? Puoi, perché i matematici riescono ancora a farne a meno. Il trucco dei matematici sta nel fatto che ci parlano sempre solo dei problemi che loro stessi possono risolvere, e non ci parlano mai di quei problemi che non possono risolvere. Vedere. Se conosciamo il risultato dell'addizione e di un termine, utilizziamo la sottrazione per trovare l'altro termine. Tutto. Non conosciamo altri problemi e non siamo in grado di risolverli. Cosa fare se conosciamo solo il risultato dell'addizione e non conosciamo entrambi i termini? In questo caso il risultato dell'addizione deve essere scomposto in due termini utilizzando funzioni angolari lineari. Inoltre, scegliamo noi stessi quale può essere un termine e le funzioni angolari lineari mostrano quale dovrebbe essere il secondo termine affinché il risultato dell'addizione sia esattamente ciò di cui abbiamo bisogno. Può esserci un numero infinito di tali coppie di termini. Nella vita di tutti i giorni facciamo benissimo senza scomporre la somma; ci basta la sottrazione. Ma negli studi scientifici sulle leggi della natura, l’espansione della somma in termini può essere molto utile.

Un'altra legge dell'addizione di cui ai matematici non piace parlare (un altro dei loro trucchi) richiede che i termini abbiano la stessa unità di misura. Per lattuga, acqua e borscht, queste possono essere unità di peso, volume, costo o unità di misura.

La figura mostra due livelli di differenza per la matematica. Il primo livello sono le differenze nel campo dei numeri, che sono indicati UN, B, C. Questo è ciò che fanno i matematici. Il secondo livello sono le differenze nell'area delle unità di misura, che sono indicate tra parentesi quadre e sono indicate dalla lettera U. Questo è ciò che fanno i fisici. Possiamo comprendere il terzo livello: le differenze nella portata degli oggetti descritti. Oggetti diversi possono avere lo stesso numero delle stesse unità di misura. Quanto sia importante, possiamo vedere l'esempio della trigonometria del borscht. Se aggiungiamo pedici alla stessa notazione per le unità di misura di oggetti diversi, possiamo dire esattamente quale quantità matematica descrive un particolare oggetto e come cambia nel tempo o in relazione alle nostre azioni. lettera W Segnerò l'acqua con la lettera S Segnerò l'insalata con la lettera B- borsch. Ecco come apparirebbero le funzioni dell'angolo lineare per il borscht.

Se prendiamo una parte dell'acqua e una parte dell'insalata, insieme si trasformeranno in una porzione di borscht. Qui ti suggerisco di prenderti una piccola pausa dal borscht e di ricordare la tua infanzia lontana. Ricordi come ci hanno insegnato a mettere insieme coniglietti e anatre? Era necessario scoprire quanti animali usciranno. Allora cosa ci è stato insegnato a fare? Ci è stato insegnato a separare le unità dai numeri e ad aggiungere numeri. Sì, qualsiasi numero può essere aggiunto a qualsiasi altro numero. Questo è un percorso diretto verso l'autismo della matematica moderna: non capiamo cosa, non è chiaro il motivo, e capiamo molto male come questo si riferisca alla realtà, a causa dei tre livelli di differenza, i matematici operano solo su uno. Sarà più corretto imparare a passare da un'unità di misura all'altra.

E i conigli, le anatre e gli animaletti possono essere contati a pezzi. Un'unità di misura comune per diversi oggetti ci consente di sommarli insieme. Questa è una versione del problema per bambini. Diamo un'occhiata a un problema simile per gli adulti. Cosa ottieni quando aggiungi coniglietti e soldi? Ci sono due possibili soluzioni qui.

Prima opzione. Determiniamo il valore di mercato dei conigli e lo aggiungiamo al denaro disponibile. Abbiamo ottenuto il valore totale della nostra ricchezza in termini di denaro.

Seconda opzione. Puoi aggiungere il numero di conigli al numero di banconote che abbiamo. Otterremo l'importo dei beni mobili in pezzi.

Come puoi vedere, la stessa legge di addizione consente di ottenere risultati diversi. Tutto dipende da cosa vogliamo sapere esattamente.

Ma torniamo al nostro borscht. Ora possiamo vedere cosa accadrà per diversi valori dell'angolo delle funzioni angolari lineari.

L'angolo è zero. Abbiamo insalata ma niente acqua. Non possiamo cucinare il borscht. Anche la quantità di borscht è zero. Ciò non significa affatto che zero borscht equivalga a zero acqua. Zero borsch può anche essere a zero insalata (angolo retto).

Per me personalmente, questa è la principale prova matematica del fatto che . Lo zero non modifica il numero quando viene aggiunto. Questo perché l'addizione stessa è impossibile se c'è un solo termine e manca il secondo. Puoi relazionarti con questo come preferisci, ma ricorda: tutte le operazioni matematiche con zero sono state inventate dai matematici stessi, quindi scarta la tua logica e riempi stupidamente le definizioni inventate dai matematici: "la divisione per zero è impossibile", "qualsiasi numero moltiplicato per zero uguale a zero", "dietro il punto zero" e altre sciocchezze. Basta ricordare una volta che lo zero non è un numero, e non avrai mai la domanda se lo zero sia un numero naturale o meno, perché una domanda del genere generalmente perde ogni significato: come si può considerare un numero ciò che non è un numero? . È come chiedere a quale colore attribuire un colore invisibile. Aggiungere zero a un numero è come dipingere con una vernice che non esiste. Hanno agitato un pennello asciutto e hanno detto a tutti che "abbiamo dipinto". Ma sto divagando un po'.

L'angolo è maggiore di zero ma inferiore a quarantacinque gradi. Abbiamo molta lattuga, ma poca acqua. Di conseguenza, otteniamo un borscht denso.

L'angolo è di quarantacinque gradi. Abbiamo la stessa quantità di acqua e lattuga. Questo è il borscht perfetto (perdonatemi i cuochi, è solo matematica).

L'angolo è maggiore di quarantacinque gradi ma inferiore a novanta gradi. Abbiamo molta acqua e poca lattuga. Prendi il borscht liquido.

Angolo retto. Abbiamo l'acqua. Della lattuga rimangono solo i ricordi, mentre continuiamo a misurare l'angolo dalla linea che un tempo segnava la lattuga. Non possiamo cucinare il borscht. La quantità di borscht è zero. In tal caso, aspetta e bevi acqua finché è disponibile)))

Qui. Qualcosa come questo. Posso raccontare altre storie qui che saranno più che appropriate qui.

I due amici partecipavano all'attività comune. Dopo l'omicidio di uno di loro, tutto è andato all'altro.

L'emergere della matematica sul nostro pianeta.

Tutte queste storie sono raccontate nel linguaggio della matematica utilizzando funzioni angolari lineari. Un'altra volta ti mostrerò il posto reale di queste funzioni nella struttura della matematica. Nel frattempo torniamo alla trigonometria del borscht e consideriamo le proiezioni.

Sabato 26 ottobre 2019

Mercoledì 7 agosto 2019

Concludendo il discorso su , dobbiamo considerare un insieme infinito. Dato che il concetto di "infinito" agisce sui matematici, come un boa constrictor su un coniglio. Il tremante orrore dell’infinito priva i matematici del buon senso. Ecco un esempio:

Si trova la fonte originale. Alpha denota un numero reale. Il segno uguale nelle espressioni precedenti indica che se aggiungi un numero o un infinito all'infinito, non cambierà nulla, il risultato sarà lo stesso infinito. Se prendiamo come esempio un insieme infinito di numeri naturali, gli esempi considerati possono essere rappresentati come segue:

Per dimostrare visivamente la loro tesi, i matematici hanno escogitato molti metodi diversi. Personalmente considero tutti questi metodi come le danze degli sciamani con i tamburelli. In sostanza, tutto si riduce al fatto che alcune stanze non sono occupate e vi vengono sistemati nuovi ospiti, oppure che alcuni visitatori vengono gettati nel corridoio per fare posto agli ospiti (molto umanamente). Ho presentato il mio punto di vista su tali decisioni sotto forma di una storia fantastica sulla Bionda. Su cosa si basa il mio ragionamento? Lo spostamento di un numero infinito di visitatori richiede una quantità infinita di tempo. Dopo che avremo lasciato la prima stanza degli ospiti, uno dei visitatori percorrerà sempre il corridoio dalla sua stanza a quella successiva fino alla fine del tempo. Naturalmente, il fattore tempo può essere stupidamente ignorato, ma questo rientrerà già nella categoria "la legge non è scritta per gli sciocchi". Tutto dipende da cosa stiamo facendo: adattare la realtà alle teorie matematiche o viceversa.

Cos'è un "hotel infinito"? Una locanda infinita è una locanda che ha sempre un numero qualsiasi di posti liberi, non importa quante stanze siano occupate. Se tutte le stanze del corridoio infinito "per i visitatori" sono occupate, c'è un altro corridoio infinito con stanze per gli "ospiti". Ci sarà un numero infinito di tali corridoi. Allo stesso tempo, l '"hotel infinito" ha un numero infinito di piani in un numero infinito di edifici su un numero infinito di pianeti in un numero infinito di universi creati da un numero infinito di Dei. I matematici, invece, non riescono a sottrarsi ai banali problemi quotidiani: Dio-Allah-Buddha è sempre uno solo, l'albergo è uno solo, il corridoio è uno solo. Così i matematici cercano di destreggiarsi tra i numeri seriali delle camere d'albergo, convincendoci che è possibile "spingere ciò che non è stato spinto".

Ti dimostrerò la logica del mio ragionamento usando l'esempio di un insieme infinito di numeri naturali. Per prima cosa devi rispondere a una domanda molto semplice: quanti insiemi di numeri naturali esistono: uno o molti? Non esiste una risposta corretta a questa domanda, poiché noi stessi abbiamo inventato i numeri, non esistono numeri in Natura. Sì, la Natura sa contare perfettamente, ma per questo utilizza altri strumenti matematici che non ci sono familiari. Come pensa la Natura, te lo dirò un'altra volta. Dato che abbiamo inventato i numeri, saremo noi stessi a decidere quanti insiemi di numeri naturali esistono. Considera entrambe le opzioni, come si addice a un vero scienziato.

Opzione uno. "Diamoci" un unico insieme di numeri naturali, che giace serenamente su uno scaffale. Prendiamo questo set dallo scaffale. Questo è tutto, non ci sono altri numeri naturali rimasti sullo scaffale e non c'è nessun posto dove portarli. Non possiamo aggiungerne uno a questo set, poiché lo abbiamo già. E se lo volessi davvero? Nessun problema. Possiamo prendere un'unità dal set che abbiamo già preso e rimetterla sullo scaffale. Successivamente, possiamo prendere un'unità dallo scaffale e aggiungerla a ciò che ci è rimasto. Di conseguenza, otteniamo nuovamente un insieme infinito di numeri naturali. Puoi scrivere tutte le nostre manipolazioni in questo modo:

Ho scritto le operazioni in notazione algebrica e in notazione della teoria degli insiemi, elencando in dettaglio gli elementi dell'insieme. Il pedice indica che abbiamo un solo ed unico insieme di numeri naturali. Si scopre che l'insieme dei numeri naturali rimarrà invariato solo se ne viene sottratto uno e ne viene aggiunto lo stesso.

Opzione due. Abbiamo sullo scaffale molti insiemi infiniti di numeri naturali. Sottolineo: DIVERSI, nonostante siano praticamente indistinguibili. Prendiamo uno di questi set. Quindi ne prendiamo uno da un altro insieme di numeri naturali e lo aggiungiamo all'insieme che abbiamo già preso. Possiamo anche sommare due insiemi di numeri naturali. Ecco cosa otteniamo:

I pedici "uno" e "due" indicano che questi elementi appartenevano a insiemi diversi. Sì, se aggiungi uno a un insieme infinito, anche il risultato sarà un insieme infinito, ma non sarà uguale all'insieme originale. Se a un insieme infinito si aggiunge un altro insieme infinito, il risultato è un nuovo insieme infinito costituito dagli elementi dei primi due insiemi.

L'insieme dei numeri naturali viene utilizzato per contare allo stesso modo di un righello per le misurazioni. Ora immagina di aver aggiunto un centimetro al righello. Questa sarà già una linea diversa, non uguale all'originale.

Puoi accettare o meno il mio ragionamento: sono affari tuoi. Ma se mai ti imbatti in problemi matematici, valuta se sei sulla strada del falso ragionamento, percorsa da generazioni di matematici. Dopotutto, le lezioni di matematica, prima di tutto, formano in noi uno stereotipo stabile del pensiero, e solo allora ci aggiungono capacità mentali (o viceversa, ci privano del libero pensiero).

pozg.ru

Domenica 4 agosto 2019

Stavo scrivendo un poscritto a un articolo sull'argomento e ho visto questo meraviglioso testo su Wikipedia:

Leggiamo: "... la ricca base teorica della matematica di Babilonia non aveva un carattere olistico e si riduceva a un insieme di tecniche disparate, prive di un sistema comune e di una base di prove".

Oh! Quanto siamo intelligenti e quanto bene riusciamo a vedere i difetti degli altri. È debole per noi guardare la matematica moderna nello stesso contesto? Parafrasando leggermente il testo sopra, personalmente ho ottenuto quanto segue:

La ricca base teorica della matematica moderna non ha un carattere olistico ed è ridotta a un insieme di sezioni disparate, prive di un sistema comune e di una base di prove.

Non andrò lontano per confermare le mie parole: ha un linguaggio e convenzioni diverse dal linguaggio e dalle convenzioni di molti altri rami della matematica. Gli stessi nomi in diversi rami della matematica possono avere significati diversi. Voglio dedicare un intero ciclo di pubblicazioni agli errori più evidenti della matematica moderna. Arrivederci.

Sabato 3 agosto 2019

Come dividere un insieme in sottoinsiemi? Per fare ciò è necessario inserire una nuova unità di misura, che è presente in alcuni elementi dell'insieme selezionato. Considera un esempio.

Possiamo averne molti UN composto da quattro persone. Questo insieme è formato sulla base delle "persone". Designiamo gli elementi di questo insieme tramite la lettera UN, il pedice con un numero indicherà il numero ordinale di ciascuna persona in questo insieme. Introduciamo una nuova unità di misura "caratteristica sessuale" e denotiamola con la lettera B. Poiché le caratteristiche sessuali sono inerenti a tutte le persone, moltiplichiamo ogni elemento dell'insieme UN sul genere B. Si noti che il nostro insieme "persone" è ora diventato l'insieme "persone con genere". Successivamente possiamo dividere i caratteri sessuali in maschili bm e quello delle donne peso corporeo caratteristiche di genere. Ora possiamo applicare un filtro matematico: selezioniamo una di queste caratteristiche sessuali, non importa quale sia maschile o femminile. Se è presente in una persona, lo moltiplichiamo per uno, se non esiste tale segno, lo moltiplichiamo per zero. E poi applichiamo la solita matematica scolastica. Guarda cosa è successo.

Dopo moltiplicazioni, riduzioni e riarrangiamenti, abbiamo ottenuto due sottoinsiemi: il sottoinsieme maschile bm e un sottoinsieme di donne peso corporeo. Più o meno allo stesso modo ragionano i matematici quando applicano nella pratica la teoria degli insiemi. Ma non ci lasciano entrare nei dettagli, ma ci danno il risultato finale: "molte persone sono costituite da un sottoinsieme di uomini e un sottoinsieme di donne". Naturalmente potresti avere una domanda: come è stata applicata correttamente la matematica nelle trasformazioni di cui sopra? Oserei assicurarti che in effetti le trasformazioni vengono eseguite correttamente, è sufficiente conoscere la giustificazione matematica dell'aritmetica, dell'algebra booleana e di altre sezioni della matematica. Cos'è? Un'altra volta te lo racconterò.

Per quanto riguarda i superset, è possibile unire due insiemi in un unico superset scegliendo un'unità di misura presente negli elementi di questi due insiemi.

Come puoi vedere, le unità di misura e la matematica comune rendono la teoria degli insiemi una cosa del passato. Un segno che non tutto va bene con la teoria degli insiemi è che i matematici hanno escogitato un proprio linguaggio e una propria notazione per la teoria degli insiemi. I matematici hanno fatto quello che una volta facevano gli sciamani. Solo gli sciamani sanno applicare "correttamente" la loro "conoscenza". Questa "conoscenza" ci insegnano.

Infine, voglio mostrarti come i matematici manipolano i dati .

Lunedì 7 gennaio 2019

Nel V secolo aC, l'antico filosofo greco Zenone di Elea formulò le sue famose aporie, la più famosa delle quali è l'aporia "Achille e la tartaruga". Ecco come suona:

Diciamo che Achille corre dieci volte più veloce della tartaruga ed è mille passi dietro di lei. Durante il tempo in cui Achille percorre questa distanza, la tartaruga striscia per cento passi nella stessa direzione. Quando Achille avrà percorso cento passi, la tartaruga ne farà altri dieci, e così via. Il processo continuerà indefinitamente, Achille non raggiungerà mai la tartaruga.

Questo ragionamento divenne uno shock logico per tutte le generazioni successive. Aristotele, Diogene, Kant, Hegel, Gilbert... Tutti, in un modo o nell'altro, consideravano le aporie di Zenone. Lo shock è stato così forte che" ... le discussioni continuano al momento, la comunità scientifica non è ancora riuscita a raggiungere un'opinione comune sull'essenza dei paradossi ... analisi matematica, teoria degli insiemi, nuovi approcci fisici e filosofici sono stati coinvolti nello studio della questione ; nessuno di loro è diventato una soluzione universalmente accettata al problema..."[Wikipedia," Aporias di Zenone "]. Tutti capiscono di essere stati ingannati, ma nessuno capisce quale sia l'inganno.

Dal punto di vista della matematica, Zenone nella sua aporia dimostrò chiaramente il passaggio dal valore all'. Questa transizione implica l'applicazione invece di costanti. Per quanto ho capito, l'apparato matematico per applicare unità di misura variabili o non è stato ancora sviluppato, oppure non è stato applicato all'aporia di Zenone. L'applicazione della nostra logica abituale ci porta in una trappola. Noi, per inerzia del pensiero, applichiamo unità di tempo costanti al reciproco. Da un punto di vista fisico, questo sembra un rallentamento del tempo fino a fermarsi completamente nel momento in cui Achille raggiunge la tartaruga. Se il tempo si ferma, Achille non potrà più raggiungere la tartaruga.

Se giriamo la logica a cui siamo abituati, tutto va a posto. Achille corre a velocità costante. Ogni segmento successivo del suo percorso è dieci volte più corto del precedente. Di conseguenza, il tempo impiegato per superarlo è dieci volte inferiore a quello precedente. Se applichiamo il concetto di "infinito" in questa situazione, allora sarebbe corretto dire "Achille raggiungerà la tartaruga con una rapidità infinita".

Come evitare questa trappola logica? Rimanere in unità di tempo costanti e non passare a valori reciproci. Nel linguaggio di Zenone, assomiglia a questo:

Nel tempo impiegato da Achille per percorrere mille passi, la tartaruga ne fa cento nella stessa direzione. Nell'intervallo di tempo successivo, uguale al primo, Achille percorrerà altri mille passi e la tartaruga ne farà cento. Adesso Achille è ottocento passi avanti alla tartaruga.

Questo approccio descrive adeguatamente la realtà senza paradossi logici. Ma questa non è una soluzione completa al problema. L'affermazione di Einstein sull'insormontabilità della velocità della luce è molto simile all'aporia di Zenone "Achille e la tartaruga". Dobbiamo ancora studiare, ripensare e risolvere questo problema. E la soluzione va cercata non nei numeri infinitamente grandi, ma nelle unità di misura.

Un'altra interessante aporia di Zenone racconta di una freccia volante:

Una freccia volante è immobile, poiché in ogni momento è a riposo, e poiché è a riposo in ogni momento, è sempre a riposo.

In questa aporia, il paradosso logico viene superato in modo molto semplice: è sufficiente chiarire che in ogni momento la freccia volante riposa in diversi punti dello spazio, il che, in effetti, è movimento. C'è un altro punto da notare qui. Da una fotografia di un'auto sulla strada, è impossibile determinare né il fatto del suo movimento né la distanza da essa. Per determinare il fatto del movimento dell'auto, sono necessarie due fotografie scattate dallo stesso punto in momenti diversi nel tempo, ma non possono essere utilizzate per determinare la distanza. Per determinare la distanza dall'auto, sono necessarie due fotografie scattate contemporaneamente da punti diversi nello spazio, ma da esse non è possibile determinare il fatto del movimento (naturalmente, hai ancora bisogno di dati aggiuntivi per i calcoli, la trigonometria ti aiuterà). Ciò che voglio sottolineare in particolare è che due punti nel tempo e due punti nello spazio sono due cose diverse che non devono essere confuse poiché forniscono diverse opportunità di esplorazione.
Mostrerò il procedimento con un esempio. Selezioniamo "rosso solido in un brufolo": questo è il nostro "tutto". Allo stesso tempo vediamo che queste cose sono con arco e ce ne sono senza arco. Successivamente, selezioniamo una parte del "tutto" e formiamo un set "con un arco". È così che gli sciamani si nutrono legando la loro teoria degli insiemi alla realtà.

Adesso facciamo un piccolo trucchetto. Prendiamo "solido in un brufolo con un fiocco" e uniamo questi "interi" per colore, selezionando gli elementi rossi. Abbiamo molto "rosso". Ora una domanda complicata: i set ricevuti "con fiocco" e "rosso" sono lo stesso set o due set diversi? Solo gli sciamani conoscono la risposta. Più precisamente, loro stessi non sanno nulla, ma come si suol dire, così sia.

Questo semplice esempio mostra che la teoria degli insiemi è completamente inutile quando si tratta di realtà. Qual è il segreto? Abbiamo formato un set di "brufoloni rossi solidi con fiocco". La formazione avveniva secondo quattro diverse unità di misura: colore (rosso), resistenza (solido), rugosità (a protuberanza), decorazioni (a fiocco). Solo un insieme di unità di misura permette di descrivere adeguatamente gli oggetti reali nel linguaggio della matematica. Ecco come appare.

La lettera "a" con indici diversi indica diverse unità di misura. Tra parentesi sono evidenziate le unità di misura in base alle quali viene assegnato il "tutto" in fase preliminare. Tra parentesi è indicata l'unità di misura in base alla quale è formato l'insieme. L'ultima riga mostra il risultato finale: un elemento del set. Come puoi vedere, se usiamo le unità per formare un insieme, il risultato non dipende dall'ordine delle nostre azioni. E questa è matematica, e non le danze degli sciamani con i tamburelli. Gli sciamani possono “intuitivamente” arrivare allo stesso risultato, argomentandolo con “ovvietà”, perché le unità di misura non sono incluse nel loro arsenale “scientifico”.

Con l'aiuto delle unità di misura, è molto semplice dividerne uno o combinare più set in un unico superset. Diamo uno sguardo più da vicino all'algebra di questo processo.

Ricordare!

Da tre membri noti della proporzione, puoi sempre trovare il suo membro sconosciuto (quarto).

risolvere la proporzione significa trovare tutti i suoi membri. Risolviamo la proporzione seguente
(trova "x").

Per trovare la "x", utilizziamo la proprietà principale della proporzione (la regola della "croce").

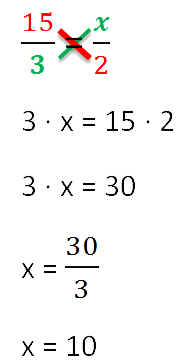
Ora siamo pronti per capire come risolvere i problemi di proporzione.

Risoluzione di problemi sulle proporzioni

Spesso compiti di proporzione strettamente legato alle percentuali. Puoi rispolverare la tua conoscenza delle percentuali nella sezione "Interessi".

Compito

Dall'arco furono sparati 50 colpi. 5 frecce volarono oltre il bersaglio. Determina la percentuale di successo.

Per tradizione, enfatizziamo i dati importanti e numerici nel problema.

Tieni presente che dobbiamo determinare la percentuale di colpi andati a segno, non la percentuale di frecce che mancano.

Pertanto, calcoliamo prima quante frecce colpiscono il bersaglio. Non sarà difficile farlo.

• 50 − 5 = 45 (frecce) - colpisci il bersaglio.

Successivamente, per risolvere il problema, creeremo una tabella in cui inseriremo tutti i dati. Ricorda che di fronte al 100% nella tabella di solito è scritto l'importo totale di qualcosa. Le percentuali sconosciute saranno indicate con la lettera x.

Per registrare correttamente i dati necessari nella tabella, ricorda una semplice regola.

L'uguaglianza di due rapporti si chiama proporzione.

a:b =c:d. Questa è proporzione. Leggere: UN quindi vale per B, Come C si riferisce a D. Numeri UN E D chiamato estremo membri della proporzione e i numeri B E C – media membri della proporzione.

Esempio di proporzione: 1 2 : 3 = 16 : 4 . Questa è l'uguaglianza di due rapporti: 12:3= 4 e 16:4= 4 . Si legge: dodici sta a tre come sedici sta a quattro. Qui 12 e 4 sono i membri estremi della proporzione, e 3 e 16 sono i membri medi della proporzione.

Proprietà fondamentale della proporzione.

Il prodotto dei termini estremi di una proporzione è uguale al prodotto dei suoi termini medi.

Per proporzione a:b =c:d O a/b=c/d la proprietà principale è scritta così: a d \u003d b c .

Per la nostra proporzione 12 : 3 = 16 : 4 la proprietà principale sarà scritta come segue: 12 4 = 3 16 . Risulta l'uguaglianza corretta: 48 \u003d 48 .

Per trovare il termine estremo sconosciuto della proporzione, è necessario dividere il prodotto dei termini medi della proporzione per il termine estremo noto.

Esempi.

1)x:20 = 2:5. Abbiamo X E 5 sono i membri estremi della proporzione, e 20 E 2 - medio.

Soluzione.

x = (20 2):5- devi moltiplicare i termini medi ( 20 E 2 ) e dividere il risultato per il termine estremo noto (numero 5 );

x=40:5è il prodotto dei termini medi ( 40 ) dividere per il termine estremo noto ( 5 );

x = 8. Abbiamo ottenuto il termine estremo desiderato della proporzione.

È più conveniente scrivere il risultato di un membro sconosciuto della proporzione utilizzando una frazione ordinaria. Ecco come verrebbe quindi scritto l’esempio che abbiamo considerato:

Il termine estremo desiderato della proporzione ( X) sarà uguale al prodotto dei termini medi ( 20 E 2 ) diviso per il termine estremo noto ( 5 ).

Riduciamo la frazione di 5 (dividi per 5 X.

Altri esempi simili di ricerca di un membro estremo sconosciuto della proporzione.

Per trovare il termine medio sconosciuto della proporzione, è necessario dividere il prodotto dei termini estremi della proporzione per il termine medio noto.

Esempi. Trova il termine medio sconosciuto della proporzione.

5) 9: x = 3: 14. Numero 3 è il termine medio noto della proporzione data, numeri 9 E 14 sono i termini estremi della proporzione.

Soluzione.

x \u003d (9 14): 3 - moltiplicare i termini estremi della proporzione e dividere il risultato per il termine medio noto della proporzione;

x= 136:3;

x=42.

La soluzione di questo esempio può essere scritta diversamente:

Il termine medio richiesto della proporzione ( X) sarà uguale al prodotto dei termini estremi ( 9 E 14 ) diviso per il termine medio noto ( 3 ).

Riduciamo la frazione di 3 (dividi per 3 e il numeratore e il denominatore di una frazione). Trovare il valore X.

Se hai dimenticato come ridurre le frazioni ordinarie, ripeti l'argomento: ""

Altri esempi simili sulla ricerca del membro medio sconosciuto della proporzione.

Sezioni: Matematica

Tipo di lezione: Lezione di studio e consolidamento primario di nuove conoscenze.

Forma della lezione: lezione-ricerca.

Obiettivi della lezione:

• attivare l'attività cognitiva degli studenti;
• introdurre gli studenti ai concetti: proporzione, membri della proporzione; proporzioni corrette e errate;
• introdurre gli studenti alle proprietà fondamentali della proporzione e formare l'abilità di determinare la proporzione corretta.

Attrezzatura:

Le schede del percorso indicano i punti che possono essere ottenuti risolvendo i compiti. Nel valutare, lo studente tiene conto della correttezza della sua decisione, della velocità della decisione (autocontrollo e controllo reciproco con l'aiuto della presentazione). Nella riga "Punti aggiuntivi", vengono assegnati punti per rispondere a domande aggiuntive, per aiutare l'insegnante a organizzare i test di altri studenti e anche per "indovinare" l'argomento della lezione.

Le cartoline vengono tagliate e distribuite in buste agli studenti (una busta per banco).

3. Schede per una lavagna magnetica (Figura 1, Figura 2, Figura 3)

Durante la lezione, queste carte vengono affisse su una lavagna magnetica.

4. Puzzle (Figura 4, Figura 5, Figura 6, Figura 7).

I rebus compilati dagli studenti delle scuole superiori (ad eccezione del rebus “Proporzione” - questo rebus è stato tratto da una lezione presentata all'FPI dall'insegnante Kozak Tatyana Ivanovna, scuola secondaria n. 20 Progress, regione dell'Amur) si trovano sul tabellone, gli studenti sono invitati a risolverli dopo la lezione.

L'attrezzatura tecnica della lezione è un computer, un proiettore per dimostrare una presentazione, uno schermo. Presentazione al computer in Microsoft PowerPoint (Appendice 4).

I. Organizzazione dell'inizio della lezione

Ciao! Controlla di avere dei fogli sulla scrivania, di avere una matita rossa e blu e di essere pronto per la lezione.

II. Argomenti del messaggio, scopi e obiettivi della lezione.

Oggi a lezione continuiamo a studiare un'ampia sezione del corso di matematica. Abbiamo finito di studiare l'argomento (cosa? - "Atteggiamento"). Ora stiamo iniziando ad esplorare un nuovo argomento in questa sezione. Alcuni esempi ci aiuteranno a comprendere l'argomento della lezione. Sul frontespizio del tuo foglio di percorso, devi compilare la tabella risolvendo oralmente gli esempi e poi conoscerai l'argomento della lezione di oggi. DIAPOSITIVA 1

Quindi, l'argomento della lezione di oggi Proporzione. DIAPOSITIVA 2

Conoscendo l'argomento della lezione, prova a creare un piano di lezione. Cosa dovresti imparare in classe oggi? Cosa vuoi sapere? Cosa vuoi imparare in classe?

Faremo un piano, che integreremo durante la lezione. (gli studenti nominano i primi due e gli ultimi due punti del programma, il resto viene compilato durante la lezione, man mano che vengono “scoperte” nuove conoscenze; ​​il programma della lezione è scritto alla lavagna)

- ripetizione (domande relative all'atteggiamento)

Definizione di proporzione

MEMBRI DI PROPORZIONE

PROPORZIONI GIUSTE E SCORRETTE

PRINCIPALI PROPRIETÀ DELLA PROPORZIONE

Applicazione in matematica

Applicazione nella vita

Potremo analizzare gli ultimi due punti nelle lezioni successive, man mano che approfondiremo l'argomento.

III. Aggiornamento delle conoscenze degli studenti. Preparazione per l'attività educativa e cognitiva attiva nella fase principale della lezione.

Discuti le domande relative all'argomento "Atteggiamento" con un compagno di classe.

Chi è pronto a porre domande relative all'ultimo argomento? (bufera di neve) MP1

- Cos'è un atteggiamento?

Come puoi scrivere una relazione?

A quali domande risponde l’atteggiamento?

Come puoi scrivere il rapporto tra due numeri?

Cosa può sostituire il segno do?

Perché pensi che abbiamo ripetuto questi concetti?

Ci aiuteranno quando impareremo un nuovo argomento.

Prendi le buste e inventa la relazione UN A B E C A D due strade. (solo 4 relazioni) LAVORO IN COPPIA.

MP2 Hai diverse relazioni davanti a te. Trova il significato di queste espressioni. DIAPOSITIVA 3

4: 0,5=
=
5: 10 =
=
8: 1 =
2,5: 5 =

Raggruppare le relazioni in base a un determinato attributo e creare le uguaglianze corrispondenti.

IV. Assimilazione di nuove conoscenze.

4: 0,5 = 8: 1

=

5: 10 = 2,5: 5

Su quale base hai raggruppato queste relazioni?

- I loro valori sono uguali.

Le uguaglianze risultanti sono chiamate proporzioni.

Pensa e definisci la proporzione.

SUGGERIMENTO: la proporzione è... SULLO SCHERMO ( uguaglianza)

Uguaglianza di …COSA ( relazioni)

Quante relazioni? ( due).

Chi è sicuro della sua opinione scriva la definizione nella scheda del percorso. MP3

Chi è pronto per andare alla lavagna e stilare una definizione di proporzione? (Appendice 3)

DEFINIZIONE (su lavagna magnetica): La proporzione è l'uguaglianza di due rapporti.

Diamo un'occhiata all'interpretazione della parola proporzione nel dizionario della lingua russa Ozhegov S.I. DIAPOSITIVA 4: “La proporzione è un certo rapporto tra le parti, proporzionalità. In matematica, l'uguaglianza di due rapporti.

Hai formulato la definizione di proporzione così come nel dizionario della lingua russa!

Pensa a quale termine matematico è in consonanza con la parola "proporzione"? ( interesse). Come si traduce il termine "percentuale"? ( da cento). Quindi "pro" è tradotto come "da". Quale parte della parola rimane? (“ una porzione"). Dove hai trovato questa parola? (in cucina) Cosa significa? ( misurare)

La parola proporzione deriva dalla parola latina proportio - proporzionalità. (dizionario etimologico). DIAPOSITIVA 4

Usando la definizione di proporzione, scrivi le proporzioni usando il segno di divisione e la barra frazionaria. (LAVORI IN COPPIA, buste).

Nei fogli di percorso, annotare la proporzione utilizzando le lettere a, b, c, d. MP4

E ora scopriremo come si chiamano i numeri che compongono la proporzione.

Numeri a, b, c, d chiamati membri della proporzione

Qual è il primo e l'ultimo termine della proporzione? ( a e c)

E quello che di solito (nella vita) viene chiamato il primo e l'ultimo? (estremo)

Quindi i termini aeb si chiamano...? (estremo)

Dove sono i termini c e d? (nel mezzo)

E come si chiamano i membri c e d? ( medio)

Quali membri sono evidenziati in rosso? ( A Presto)

colore (Con raro) membri.

membri intermedi

Torniamo al programma della lezione: hai qualcosa da aggiungere? (membri estremi e medi della proporzione)

V. Consolidamento primario della conoscenza

MP5 Compila la tabella:

Quale conclusione si può trarre? Registrare l'output sull'itinerario. ( In proporzione, il prodotto dei termini estremi è uguale al prodotto dei termini medi)DIAPOSITIVA 8

MP6 Ecco cinque uguaglianze. Sono tutte proporzioni?

Enfatizza le proporzioni.

= ; 7 + 11 = 36: 2; 72: 9 = 16: 2; = 20: 4; 5 40 = 100 2

DIAPOSITIVA 7 Alzati, chi ha finito.

Sono tutti sicuri che ci siano tre proporzioni qui? Infatti, nell'ultima uguaglianza, il prodotto dei termini estremi non è uguale al prodotto di quelli medi. Torniamo alla definizione di proporzione ( Proporzione: l'uguaglianza di due rapporti). La terza uguaglianza è l’uguaglianza delle due relazioni? (È). Per definizione, è una proporzione? (SÌ). Il prodotto dei termini estremi è uguale al prodotto dei termini medi? (NO). Quindi è una proporzione...? (sbagliato). Questa proporzione è chiamata errata. Quindi ci sono proporzioni errate e...? (fedele). Formulare la proprietà principale della proporzione, utilizzando le conoscenze acquisite. (Nella giusta proporzione, il prodotto dei termini estremi è uguale al prodotto di quelli medi).

VI. Consolidamento della conoscenza.

Compila la tabella.

Proporzione corretta Proporzione sbagliata

=

= 20: 4

In quale altro modo puoi determinare la proporzione giusta o quella sbagliata? (trova il valore della relazione)

In futuro parleremo delle proporzioni corrette.

Torniamo al programma della lezione. Cosa si può aggiungere? (proporzioni corrette e errate)

MP7 Utilizzando le lettere B e H, segna le proporzioni corrette e quelle sbagliate.

=		1: 0,5 = 4,8: 2,4
7,5: 5 = 2: 3		=
10: 3 = 3 : 1		5:x = 20:4x

VII. Generalizzazione e sistematizzazione.

MP8 Usando la proprietà base della proporzione, componi la proporzione corretta dai seguenti numeri: 4, 5, 12, 15. Quante proporzioni corrette puoi creare?

VIII. Controllo e autoverifica delle conoscenze

MP9 Dettatura matematica

1. Annota la proporzione: il numero 18 sta a 4 come 27 sta a 6.
2. Annota la proporzione: il rapporto tra tre e cinque è uguale al rapporto tra due e sette.
3. Annota i termini medi della proporzione: 1,5: 2 \u003d 4,5: 6
4. Annota i membri estremi della proporzione: 2/1,9 = 3/2,8
5. La proporzione nel punto 3 è corretta?
6. La proporzione al punto 4 è corretta?
7. L'affermazione è vera: la radice dell'equazione è 20/5 \u003d x / 0,5 numero 2
8. È vera la seguente affermazione: quattro numeri naturali qualsiasi possono essere usati per formare una proporzione?

DIAPOSITIVA 10. Revisione tra pari

IX. Riassumendo la lezione.

Si prega di fare riferimento al programma delle lezioni.

Cosa hai imparato in classe oggi? (cos'è una proporzione, in cosa consiste una proporzione, le proporzioni sono vere e sbagliate, la proprietà principale di una proporzione, ...)

Cosa hai imparato in classe oggi? (determinare i membri estremi e medi della proporzione, scoprire se la proporzione è corretta o errata, ...)

Quali altre domande si possono porre alla fine della lezione?

-Quante proporzioni corrette si possono ricavare da questa proporzione corretta?

Come puoi sapere se una proporzione è giusta o sbagliata?

Ricordiamo l'ultimo compito del dettato matematico.

Per formare una proporzione è possibile utilizzare quattro numeri naturali qualsiasi. La risposta corretta è SI. Puoi elaborare una proporzione, ma non sarà necessariamente vera.

Dalla frase " Per formare una proporzione è possibile utilizzare quattro numeri naturali qualsiasi. Elimina una parola per rendere questa affermazione errata. (naturale). Perché? (Il numero 0 non può essere membro di una proporzione). Per formare una proporzione è possibile utilizzare quattro numeri qualsiasi

In questa frase Per formare una proporzione è possibile utilizzare quattro numeri naturali qualsiasi. inserisci una parola per rendere errata l'affermazione (VERO). Da quattro numeri naturali qualsiasi, puoi creare la proporzione corretta.

Calcola il numero di punti che hai guadagnato nella lezione e assegna un voto.

X. Informazioni sui compiti e istruzioni su come completarli

Matematica - 6, Vilenkin N.Ya. et al.6a edizione

P.21, nn. 760, 781, 782, 783 (a)

Il rapporto tra due numeri

Definizione 1

Il rapporto tra due numeriè il loro privato.

Esempio 1

il rapporto tra $18$ e $3$ può essere scritto come:

$18\div3=\frac(18)(3)=6$.

il rapporto tra $5$ e $15$ può essere scritto come:

$5\div15=\frac(5)(15)=\frac(1)(3)$.

Usando rapporto tra due numeri può essere mostrato:

• quante volte un numero è maggiore di un altro;
• quale parte rappresenta un numero da un altro.

Quando si calcola il rapporto tra due numeri al denominatore di una frazione, annotare il numero con cui viene effettuato il confronto.

Molto spesso, tale numero segue le parole "rispetto a ..." o la preposizione "a ...".

Richiama la proprietà di base di una frazione e applicala a una relazione:

Osservazione 1

Moltiplicando o dividendo entrambi i termini della relazione per lo stesso numero diverso da zero, otteniamo un rapporto uguale a quello originale.

Considera un esempio che illustra l'uso del concetto di rapporto tra due numeri.

Esempio 2

La quantità di precipitazioni nel mese precedente è stata di $195$ mm, mentre nel mese corrente è stata di $780$ mm. Quanto è aumentata la quantità di precipitazioni nel mese corrente rispetto al mese precedente?

Soluzione.

Componi il rapporto tra la quantità di precipitazioni del mese corrente e la quantità di precipitazioni del mese precedente:

$\frac(780)(195)=\frac(780\div 5)(195\div 5)=\frac(156\div 3)(39\div 3)=\frac(52)(13)=4 $.

Risposta: la quantità di precipitazioni nel mese corrente è $4$ volte superiore rispetto al mese precedente.

Esempio 3

Trova quante volte il numero $1 \frac(1)(2)$ è contenuto nel numero $13 \frac(1)(2)$.

Soluzione.

$13 \frac(1)(2)\div 1 \frac(1)(2)=\frac(27)(2)\div \frac(3)(2)=\frac(27)(2) \cdot \frac(2)(3)=\frac(27)(3)=9$.

Risposta: $ 9 $ volte.

Il concetto di proporzione

Definizione 2

Proporzione si chiama uguaglianza di due relazioni:

$a\div b=c\div d$

$\frac(a)(b)=\frac(c)(d)$.

Esempio 4

$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,

$\frac(8)(2)=\frac(36)(9)$, $\frac(10)(40)=\frac(9)(36)$, $\frac(15)(75)= \frac(1)(5)$.

Nella proporzione $\frac(a)(b)=\frac(c)(d)$ (o $a:b = c\div d$), i numeri a e d si chiamano membri estremi proporzioni, mentre i numeri $b$ e $c$ lo sono membri intermedi proporzioni.

La proporzione corretta può essere convertita come segue:

Osservazione 2

Il prodotto dei termini estremi della proporzione corretta è uguale al prodotto dei termini medi:

$a \cdot d=b \cdot c$.

Questa affermazione è proprietà fondamentale della proporzione.

È vero anche il contrario:

Osservazione 3

Se il prodotto dei termini estremi di una proporzione è uguale al prodotto dei suoi termini medi, allora la proporzione è corretta.

Osservazione 4

Se i termini medi o i termini estremi vengono riordinati nella proporzione corretta, anche le proporzioni che si otterranno saranno corrette.

Esempio 5

$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,

$\frac(2)(8)=\frac(9)(36)$, $\frac(40)(10)=\frac(36)(9)$, $\frac(75)(15)= \frac(5)(1)$.

Usando questa proprietà, è facile trovare un termine sconosciuto da una proporzione se gli altri tre sono noti:

$a=\frac(b \cdot c)(d)$; $b=\frac(a \cdot d)(c)$; $c=\frac(a \cdot d)(b)$; $d=\frac(b \cdot c)(a)$.

Esempio 6

$\frac(6)(a)=\frac(16)(8)$;

$6 \cdot 8=16 \cdot a$;

$16 \cdot a=6 \cdot 8$;

$16 \cdot a=48$;

$a=\frac(48)(16)$;

Esempio 7

$\frac(a)(21)=\frac(8)(24)$;

$a \cdot 24=21 \cdot 8$;

$a \cdot 24=168$;

$a=\frac(168)(24)$;

giardiniere $ 3 - alberi $ 108;

$x$ giardinieri - albero da $252$.

Facciamo una proporzione:

$\frac(3)(x)=\frac(108)(252)$.

Usiamo la regola per trovare il termine sconosciuto della proporzione:

$b=\frac(a \cdot d)(c)$;

$x=\frac(3 \cdot 252)(108)$;

$x=\frac(252)(36)$;

Risposta: Ci vorranno giardinieri da 7$ per potare alberi da 252$.

Molto spesso, le proprietà della proporzione vengono utilizzate nella pratica nei calcoli matematici nei casi in cui è necessario calcolare il valore di un membro sconosciuto della proporzione, se i valori degli altri tre membri sono noti.