Kaip sudaryti tinkamą proporciją. Kaip apskaičiuoti proporciją. Kaip išspręsti problemą naudojant proporcijas

Paprasčiau tariant, tai daržovės, virtos vandenyje pagal specialų receptą. Apsvarstysiu du pradinius komponentus (daržovių salotas ir vandenį) ir galutinį rezultatą - barščius. Geometriškai tai galima pavaizduoti kaip stačiakampį, kurio viena pusė žymi salotas, kita pusė – vandenį. Šių dviejų pusių suma žymės barščius. Tokio „barščių“ stačiakampio įstrižainė ir plotas yra grynai matematinės sąvokos ir niekada nenaudojamos barščių receptuose.

Kaip matematine prasme salotos ir vanduo virsta barščiais? Kaip dviejų atkarpų suma gali virsti trigonometrija? Norėdami tai suprasti, mums reikia linijinių kampų funkcijų.

Matematikos vadovėliuose nieko nerasite apie tiesinio kampo funkcijas. Bet be jų negali būti matematikos. Matematikos dėsniai, kaip ir gamtos dėsniai, veikia nepriklausomai nuo to, ar žinome, kad jie egzistuoja, ar ne.

Tiesinės kampinės funkcijos yra sudėjimo dėsniai. Pažiūrėkite, kaip algebra virsta geometrija, o geometrija – trigonometrija.

Ar galima apsieiti be linijinių kampinių funkcijų? Galite, nes matematikai vis tiek apsieina be jų. Matematikos gudrybė slypi tame, kad jie mums visada pasakoja tik apie tas problemas, kurias gali išspręsti patys, ir niekada nepasakoja apie tas problemas, kurių negali išspręsti. Matyti. Jei žinome pridėjimo ir vieno nario rezultatą, kitam dėmeniui rasti naudojame atimtį. Visi. Kitų problemų nežinome ir nesugebame jų išspręsti. Ką daryti, jei žinome tik pridėjimo rezultatą ir nežinome abiejų terminų? Šiuo atveju sudėjimo rezultatas turi būti išskaidytas į du terminus, naudojant tiesines kampines funkcijas. Be to, mes patys pasirenkame, koks gali būti vienas narys, o tiesinės kampinės funkcijos parodo, koks turėtų būti antrasis narys, kad pridėjimo rezultatas būtų būtent toks, kokio mums reikia. Tokių terminų porų gali būti be galo daug. Kasdieniame gyvenime mums puikiai sekasi neskaidydami sumos, mums užtenka atimties. Tačiau moksliniuose gamtos dėsnių tyrimuose sumos išplėtimas į terminus gali būti labai naudingas.

Kitas papildymo dėsnis, apie kurį matematikai nemėgsta kalbėti (dar vienas jų triukas), reikalauja, kad terminai turėtų tą patį matavimo vienetą. Salotoms, vandeniui ir barščiams tai gali būti svorio, tūrio, kainos ar matavimo vienetai.

Paveiksle pavaizduoti du matematikos skirtumo lygiai. Pirmasis lygis yra skaičių lauko skirtumai, kurie yra nurodyti a, b, c. Taip daro matematikai. Antrasis lygis yra matavimo vienetų ploto skirtumai, kurie rodomi laužtiniuose skliaustuose ir yra pažymėti raide U. Taip daro fizikai. Galime suprasti trečiąjį lygmenį – aprašomų objektų apimties skirtumus. Skirtingi objektai gali turėti tą patį skaičių tų pačių matavimo vienetų. Kaip tai svarbu, galime pamatyti barščių trigonometrijos pavyzdyje. Jei prie to paties žymėjimo pridėsime skirtingų objektų matavimo vienetų apatinius indeksus, galime tiksliai pasakyti, koks matematinis dydis apibūdina konkretų objektą ir kaip jis kinta laikui bėgant arba dėl mūsų veiksmų. laišką W Vandenį pažymėsiu raide S Salotas pažymėsiu raide B- barščiai. Štai kaip atrodytų barščių linijinio kampo funkcijos.

Jei paimsime dalį vandens ir dalį salotų, kartu jos pavirs į vieną barščių porciją. Čia siūlau šiek tiek pailsėti nuo barščių ir prisiminti tolimą vaikystę. Prisimeni, kaip mus mokė surišti zuikius ir antis? Reikėjo išsiaiškinti, kiek gyvulių pasirodys. Ko tada buvome išmokyti daryti? Mus mokė atskirti vienetus nuo skaičių ir sudėti skaičius. Taip, bet kurį skaičių galima pridėti prie bet kurio kito skaičiaus. Tai tiesus kelias į šiuolaikinės matematikos autizmą – mes nesuprantame ką, neaišku kodėl ir labai prastai suprantame, kaip tai susiję su realybe, nes dėl trijų skirtumo lygių matematikai operuoja tik vienu. Teisingiau bus išmokti pereiti nuo vieno matavimo vieneto prie kito.

Ir zuikius, ir antis, ir gyvūnėlius galima suskaičiuoti į gabalus. Vienas bendras skirtingų objektų matavimo vienetas leidžia juos sujungti. Tai vaikiška problemos versija. Pažvelkime į panašią suaugusiųjų problemą. Ką gausite pridėję zuikius ir pinigų? Čia yra du galimi sprendimai.

Pirmas variantas. Nustatome zuikių rinkos vertę ir pridedame prie turimų grynųjų pinigų. Mes gavome bendrą mūsų turto vertę pinigais.

Antras variantas. Prie mūsų turimų banknotų skaičiaus galite pridėti zuikių skaičių. Kilnojamojo turto kiekį gausime vienetais.

Kaip matote, tas pats papildymo įstatymas leidžia gauti skirtingus rezultatus. Viskas priklauso nuo to, ką tiksliai norime žinoti.

Bet grįžkime prie mūsų barščių. Dabar matome, kas nutiks skirtingoms linijinio kampo funkcijų kampo vertėms.

Kampas lygus nuliui. Turime salotų, bet ne vandens. Mes nemokame virti barščių. Barščių kiekis taip pat lygus nuliui. Tai visai nereiškia, kad nulis barščių yra lygus nuliui vandens. Nulinis barštis gali būti ir prie nulio salotų (stačiu kampu).

Man asmeniškai tai yra pagrindinis matematinis įrodymas, kad . Nulis nekeičia skaičiaus, kai pridedamas. Taip yra todėl, kad pats papildymas neįmanomas, jei yra tik vienas narys, o antrojo nėra. Galite su tuo susieti kaip norite, bet atminkite – visas matematines operacijas su nuliu sugalvojo patys matematikai, todėl meskite savo logiką ir kvailai kimškite matematikų sugalvotus apibrėžimus: „dalyti iš nulio neįmanoma“, „bet koks skaičius padaugintas iš nulio lygus nuliui“, „už nulio taško“ ir kitos nesąmonės. Pakanka vieną kartą prisiminti, kad nulis nėra skaičius, ir jums niekada nekils klausimų, ar nulis yra natūralusis skaičius, ar ne, nes toks klausimas paprastai praranda prasmę: kaip galima laikyti skaičių tuo, kuris nėra skaičius . Tai tarsi klausti, kokiai spalvai priskirti nematomą spalvą. Nulio pridėjimas prie skaičiaus yra tarsi tapymas dažais, kurių nėra. Jie mostelėjo sausu teptuku ir visiems sako, kad „nudažėme“. Bet aš šiek tiek nukrypstu.

Kampas yra didesnis nei nulis, bet mažesnis nei keturiasdešimt penki laipsniai. Turime daug salotų, bet mažai vandens. Dėl to gauname tirštus barščius.

Kampas yra keturiasdešimt penki laipsniai. Vandens ir salotų turime vienodus kiekius. Tai tobuli barščiai (tegu atleidžia virėjai, tai tik matematika).

Kampas yra didesnis nei keturiasdešimt penki laipsniai, bet mažesnis nei devyniasdešimt laipsnių. Turime daug vandens ir mažai salotų. Gaukite skystų barščių.

Tiesus kampas. Turime vandens. Iš salotų liko tik prisiminimai, nes toliau matuojame kampą nuo linijos, kuri kadaise žymėjo salotas. Mes nemokame virti barščių. Barščių kiekis lygus nuliui. Tokiu atveju palaikykite ir gerkite vandens, kol jo yra)))

Čia. Kažkas panašaus į tai. Čia galiu papasakoti kitų istorijų, kurios čia bus daugiau nei tinkamos.

Du draugai turėjo savo akcijų bendrame versle. Po vieno iš jų nužudymo viskas atiteko kitam.

Matematikos atsiradimas mūsų planetoje.

Visos šios istorijos pasakojamos matematikos kalba naudojant tiesines kampines funkcijas. Kada nors kitą kartą parodysiu tikrąją šių funkcijų vietą matematikos struktūroje. Tuo tarpu grįžkime prie barščių trigonometrijos ir apsvarstykime projekcijas.

Šeštadienis, 2019 m. spalio 26 d

2019 m. rugpjūčio 7 d., trečiadienis

Baigdami pokalbį apie , turime apsvarstyti begalinį rinkinį. Atsižvelgta į tai, kad „begalybės“ sąvoka veikia matematikus, kaip boa susiaurėjimas triušį. Virpantis begalybės siaubas atima iš matematikų sveiką protą. Štai pavyzdys:

Pradinis šaltinis yra. Alfa žymi realųjį skaičių. Lygybės ženklas aukščiau pateiktose išraiškose rodo, kad jei prie begalybės pridėsite skaičių arba begalybę, niekas nepasikeis, rezultatas bus ta pati begalybė. Jei kaip pavyzdį paimsime begalinę natūraliųjų skaičių aibę, nagrinėjamus pavyzdžius galima pavaizduoti taip:

Norėdami vizualiai įrodyti savo atvejį, matematikai sugalvojo daugybę skirtingų metodų. Asmeniškai aš į visus šiuos metodus žiūriu kaip į šamanų šokius su tamburinais. Iš esmės jie visi susiveda į tai, kad arba kai kurie kambariai yra neapgyvendinti ir juose įsikuria nauji svečiai, arba dalis lankytojų išmeta į koridorių, kad būtų vietos svečiams (labai žmogiškai). Savo požiūrį į tokius sprendimus pateikiau fantastiškos istorijos apie blondinę forma. Kuo remiasi mano samprotavimai? Perkelti begalinį lankytojų skaičių užtrunka be galo daug laiko. Kai atlaisvinsime pirmąjį svečių kambarį, vienas iš lankytojų visada eis koridoriumi iš savo kambario į kitą iki laiko pabaigos. Žinoma, laiko faktorių galima kvailai ignoruoti, bet tai jau bus iš kategorijos „įstatymas ne kvailiams parašytas“. Viskas priklauso nuo to, ką mes darome: prideriname tikrovę prie matematinių teorijų ar atvirkščiai.

Kas yra „begalinis viešbutis“? Infinity Inn yra užeiga, kurioje visada yra bet koks laisvų vietų skaičius, nesvarbu, kiek kambarių yra užimta. Jei begaliniame „lankytojams“ koridoriuje visi kambariai užimti, yra dar vienas begalinis prieškambaris su patalpomis „svečiams“. Tokių koridorių bus be galo daug. Tuo pačiu metu „begalinis viešbutis“ turi begalinį aukštų skaičių begaliniame pastatų skaičiuje begaliniame skaičiuje planetų begaliniame skaičiuje visatų, sukurtų begalinio skaičiaus dievų. Matematikai, atvirkščiai, nesugeba atitolti nuo banalių kasdienių problemų: Dievas-Allah-Buda visada tik vienas, viešbutis – vienas, koridorius – tik vienas. Tad matematikai bando žongliruoti viešbučių kambarių eilės numeriais, įtikinėdami, kad galima „nustumdyti nepastumdytus“.

Savo samprotavimų logiką jums parodysiu naudodamas begalinės natūraliųjų skaičių aibės pavyzdį. Pirmiausia reikia atsakyti į labai paprastą klausimą: kiek natūraliųjų skaičių aibių egzistuoja – vienas ar daug? Nėra teisingo atsakymo į šį klausimą, nes mes patys sugalvojome skaičius, gamtoje skaičių nėra. Taip, Gamta puikiai moka skaičiuoti, tačiau tam ji naudoja kitus mums nepažįstamus matematinius įrankius. Kaip gamta galvoja, pasakysiu kitą kartą. Kadangi mes išradome skaičius, mes patys nuspręsime, kiek natūraliųjų skaičių aibių yra. Apsvarstykite abu variantus, kaip ir dera tikram mokslininkui.

Variantas vienas. „Duokite mums“ vieną natūraliųjų skaičių rinkinį, kuris ramiai guli lentynoje. Šį rinkinį paimame iš lentynos. Tai tiek, kitų natūraliųjų skaičių lentynoje neliko ir nėra kur imti. Negalime jo pridėti prie šio rinkinio, nes jį jau turime. O jeigu tu tikrai to nori? Jokiu problemu. Galime paimti vienetą iš jau paimto rinkinio ir grąžinti į lentyną. Po to galime paimti vienetą iš lentynos ir pridėti prie to, kas liko. Dėl to vėl gauname begalinę natūraliųjų skaičių aibę. Visas mūsų manipuliacijas galite parašyti taip:

Veiksmus surašiau algebriniu ir aibių teorijos žymėjimu, detaliai išvardijau aibės elementus. Indeksas rodo, kad turime vieną ir vienintelį natūraliųjų skaičių rinkinį. Pasirodo, natūraliųjų skaičių aibė išliks nepakitusi tik iš jos atėmus vieną ir pridėjus tą patį.

Antras variantas. Lentynoje turime daugybę skirtingų begalinių natūraliųjų skaičių rinkinių. Pabrėžiu – SKIRTINGI, nepaisant to, kad jie praktiškai nesiskiria. Mes paimame vieną iš šių rinkinių. Tada paimame vieną iš kitos natūraliųjų skaičių aibės ir pridedame prie jau paimtos aibės. Galime pridėti net dvi natūraliųjų skaičių aibes. Štai ką mes gauname:

Indeksai „vienas“ ir „du“ rodo, kad šie elementai priklausė skirtingiems rinkiniams. Taip, jei pridėsite vieną prie begalinės aibės, rezultatas taip pat bus begalinis aibė, tačiau jis nebus toks pat kaip pradinis rinkinys. Jei prie vienos begalinės aibės pridedama kita begalinė aibė, gaunama nauja begalinė aibė, susidedanti iš pirmųjų dviejų aibių elementų.

Natūraliųjų skaičių aibė naudojama skaičiuojant taip pat, kaip ir matavimų liniuotė. Dabar įsivaizduokite, kad prie liniuotės pridėjote vieną centimetrą. Tai jau bus kita eilutė, neprilygsta originalui.

Galite priimti arba nepriimti mano samprotavimų – tai jūsų pačių reikalas. Bet jei kada nors susidursite su matematinėmis problemomis, pagalvokite, ar einate klaidingų samprotavimų keliu, kurį minti matematikų kartos. Mat matematikos pamokos pirmiausia mumyse formuoja stabilų mąstymo stereotipą, o tik tada prideda mums protinių gebėjimų (arba atvirkščiai – atima laisvą mąstymą).

pozg.ru

2019 m. rugpjūčio 4 d., sekmadienis

Rašiau poraštį straipsniui apie ir pamačiau šį nuostabų tekstą Vikipedijoje:

Skaitome: „... turtingas Babilono matematikos teorinis pagrindas neturėjo holistinio pobūdžio ir buvo sumažintas iki skirtingų metodų rinkinio, neturinčio bendros sistemos ir įrodymų bazės“.

Oho! Kokie mes protingi ir kaip gerai matome kitų trūkumus. Ar mums silpna žiūrėti į šiuolaikinę matematiką tame pačiame kontekste? Šiek tiek perfrazuodamas aukščiau pateiktą tekstą, aš asmeniškai gavau štai ką:

Turtingas šiuolaikinės matematikos teorinis pagrindas neturi holistinio pobūdžio ir yra sumažintas iki skirtingų skyrių rinkinio, neturinčio bendros sistemos ir įrodymų bazės.

Toli nepatvirtinsiu savo žodžių – jis turi kalbą ir sutartines, kurios skiriasi nuo daugelio kitų matematikos šakų kalbos ir susitarimų. Tie patys pavadinimai skirtingose matematikos šakose gali turėti skirtingas reikšmes. Visą publikacijų ciklą noriu skirti ryškiausioms šiuolaikinės matematikos klaidoms. Greitai pasimatysime.

Šeštadienis, 2019 m. rugpjūčio 3 d

Kaip aibę padalyti į poaibius? Norėdami tai padaryti, turite įvesti naują matavimo vienetą, kuris yra kai kuriuose pasirinkto rinkinio elementuose. Apsvarstykite pavyzdį.

Tegul turime daug A susidedantis iš keturių žmonių. Šis rinkinys sudarytas remiantis „žmonėmis“ Pažymėkime šio rinkinio elementus raide A, indeksas su skaičiumi nurodys kiekvieno šio rinkinio asmens eilės numerį. Įveskime naują matavimo vienetą „lytinė savybė“ ir pažymėkime jį raide b. Kadangi seksualinės savybės būdingos visiems žmonėms, mes padauginame kiekvieną rinkinio elementą A dėl lyties b. Atkreipkite dėmesį, kad mūsų rinkinys „žmonės“ dabar tapo rinkiniu „žmonės su lytimi“. Po to seksualines savybes galime suskirstyti į vyriškas bm ir moterų bw lyties ypatumai. Dabar galime pritaikyti matematinį filtrą: pasirenkame vieną iš šių seksualinių savybių, nesvarbu, kuri iš jų yra vyras ar moteris. Jei žmoguje yra, tai dauginame iš vieneto, jei tokio ženklo nėra, dauginame iš nulio. Ir tada taikome įprastą mokyklinę matematiką. Pažiūrėkite, kas atsitiko.

Po padauginimo, sumažinimų ir pertvarkymų gavome du poaibius: vyriškąjį bm ir moterų pogrupis bw. Maždaug taip pat samprotauja matematikai, taikydami aibių teoriją praktikoje. Tačiau jie neįleidžia mūsų į smulkmenas, o pateikia galutinį rezultatą – „daug žmonių susideda iš vyrų ir moterų pogrupio“. Natūralu, kad jums gali kilti klausimas, kaip teisingai pritaikė matematiką aukščiau pateiktose transformacijose? Drįstu patikinti, kad iš tikrųjų transformacijos atliekamos teisingai, užtenka žinoti aritmetikos, Būlio algebros ir kitų matematikos skyrių matematinį pagrindimą. Kas tai yra? Kažkada apie tai papasakosiu.

Kalbant apie superrinkinius, galima sujungti du rinkinius į vieną superrinkinį, pasirenkant matavimo vienetą, kuris yra šių dviejų rinkinių elementuose.

Kaip matote, matavimo vienetai ir įprasta matematika aibių teoriją paverčia praeitimi. Požymis, kad su aibių teorija ne viskas gerai, yra tai, kad matematikai sugalvojo savo kalbą ir žymėjimą aibių teorijai. Matematikai darė tai, ką kadaise darė šamanai. Tik šamanai moka „teisingai“ pritaikyti savo „žinias“. Šių „žinių“ jie mus moko.

Galiausiai noriu parodyti, kaip matematikai manipuliuoja .

Pirmadienis, 2019 m. sausio 7 d

Penktame amžiuje prieš Kristų senovės graikų filosofas Zenonas iš Elėjos suformulavo savo garsiąsias aporijas, iš kurių garsiausia yra aporija „Achilas ir vėžlys“. Štai kaip tai skamba:

Tarkime, Achilas bėga dešimt kartų greičiau už vėžlį ir nuo jo atsilieka tūkstančiu žingsnių. Per tą laiką, per kurį Achilas nubėga šį atstumą, vėžlys nušliaužia šimtą žingsnių ta pačia kryptimi. Kai Achilas nubėgs šimtą žingsnių, vėžlys nuropos dar dešimt žingsnių ir t.t. Procesas tęsis neribotą laiką, Achilas niekada nepasivys vėžlio.

Šis samprotavimas tapo logišku šoku visoms vėlesnėms kartoms. Aristotelis, Diogenas, Kantas, Hegelis, Gilbertas... Visi jie vienaip ar kitaip laikė Zenono aporijomis. Šokas buvo toks stiprus, kad " ... diskusijos tebesitęsia ir šiuo metu, mokslo bendruomenei dar nepavyko susidaryti bendros nuomonės apie paradoksų esmę ... nagrinėjant klausimą buvo įtraukta matematinė analizė, aibių teorija, nauji fizikiniai ir filosofiniai požiūriai. ; nė vienas iš jų netapo visuotinai priimtu problemos sprendimu..."[Wikipedia," Zenono Aporijos "]. Visi supranta, kad yra kvailinami, bet niekas nesupranta, kas yra apgaulė.

Matematikos požiūriu Zenonas savo aporijoje aiškiai pademonstravo perėjimą nuo vertės prie. Šis perėjimas reiškia, kad reikia taikyti vietoj konstantų. Kiek suprantu, matematinis aparatas kintamiems matavimo vienetams taikyti arba dar nėra sukurtas, arba nepritaikytas Zenono aporijai. Įprastos logikos taikymas įveda mus į spąstus. Mes pagal mąstymo inerciją abipusiam koeficientui taikome pastovius laiko vienetus. Fiziniu požiūriu tai atrodo kaip laiko sulėtėjimas, kol jis visiškai sustoja tuo metu, kai Achilas pasiveja vėžlį. Jei laikas sustoja, Achilas nebegali aplenkti vėžlio.

Jei pasukame įprastą logiką, viskas stoja į savo vietas. Achilas bėga pastoviu greičiu. Kiekvienas paskesnis jo kelio segmentas yra dešimt kartų trumpesnis nei ankstesnis. Atitinkamai, laikas, skirtas jai įveikti, yra dešimt kartų mažesnis nei ankstesnis. Jei šioje situacijoje pritaikytume „begalybės“ sąvoką, tai būtų teisinga sakyti „Achilas be galo greitai aplenks vėžlį“.

Kaip išvengti šių loginių spąstų? Laikykitės pastovių laiko vienetų ir neperjunkite prie abipusių verčių. Zenono kalba tai atrodo taip:

Per tą laiką, kurio Achilui reikia nubėgti tūkstantį žingsnių, vėžlys nušliaužia šimtą žingsnių ta pačia kryptimi. Per kitą laiko intervalą, lygų pirmajam, Achilas nubėgs dar tūkstantį žingsnių, o vėžlys nuropos šimtą žingsnių. Dabar Achilas aštuoniais šimtais žingsnių lenkia vėžlį.

Šis požiūris adekvačiai apibūdina tikrovę be jokių loginių paradoksų. Tačiau tai nėra visiškas problemos sprendimas. Einšteino teiginys apie šviesos greičio neįveikiamumą labai panašus į Zenono aporiją „Achilas ir vėžlys“. Dar turime išstudijuoti, permąstyti ir išspręsti šią problemą. Ir sprendimo reikia ieškoti ne be galo dideliais skaičiais, o matavimo vienetais.

Kita įdomi Zenono aporija pasakoja apie skrendančią strėlę:

Skraidanti strėlė yra nejudanti, nes kiekvienu laiko momentu ji yra ramybės būsenoje, o kadangi ji ilsisi kiekvienu laiko momentu, ji visada yra ramybės būsenoje.

Šioje aporijoje loginis paradoksas įveikiamas labai paprastai – užtenka patikslinti, kad kiekvienu laiko momentu skraidanti strėlė ilsisi skirtinguose erdvės taškuose, o tai iš tikrųjų yra judėjimas. Čia reikia pažymėti dar vieną dalyką. Iš vienos automobilio nuotraukos kelyje neįmanoma nustatyti nei jo judėjimo fakto, nei atstumo iki jo. Norint nustatyti automobilio judėjimo faktą, reikalingos dvi nuotraukos, darytos iš to paties taško skirtingu laiku, tačiau jomis negalima nustatyti atstumo. Norėdami nustatyti atstumą iki automobilio, jums reikia dviejų nuotraukų, padarytų iš skirtingų erdvės taškų vienu metu, tačiau iš jų negalite nustatyti judėjimo fakto (natūralu, kad jums vis tiek reikia papildomų duomenų skaičiavimams, trigonometrija jums padės). Visų pirma noriu pabrėžti, kad du laiko taškai ir du erdvės taškai yra du skirtingi dalykai, kurių nereikėtų painioti, nes jie suteikia skirtingas tyrinėjimo galimybes.
Procesą parodysiu pavyzdžiu. Renkamės „raudona kieta spuogelyje“ – tai mūsų „visa“. Tuo pačiu matome, kad šie dalykai yra su lanku, o yra be lanko. Po to išrenkame dalį „visumos“ ir suformuojame rinkinį „su lanku“. Taip šamanai maitinasi, susiedami savo aibių teoriją su realybe.

Dabar padarykime nedidelį triuką. Paimkime „kietą spuogelyje su lanku“ ir sujungsime šiuos „visumus“ pagal spalvą, parinkdami raudonus elementus. Gavome daug „raudonos“. Dabar sudėtingas klausimas: ar gauti rinkiniai „su lanku“ ir „raudona“ yra tas pats rinkinys, ar du skirtingi rinkiniai? Tik šamanai žino atsakymą. Tiksliau, jie patys nieko nežino, bet kaip sako, taip ir yra.

Šis paprastas pavyzdys rodo, kad aibių teorija yra visiškai nenaudinga, kai kalbama apie tikrovę. Kokia paslaptis? Suformavome rinkinį „raudoną kietą spuogelį su lankeliu“. Formavimas vyko pagal keturis skirtingus matavimo vienetus: spalvą (raudona), stiprumą (vientisą), šiurkštumą (spuogelyje), dekoracijas (su lanku). Tik matavimo vienetų rinkinys leidžia matematikos kalba adekvačiai apibūdinti tikrus objektus. Štai kaip tai atrodo.

Raidė „a“ su skirtingais indeksais žymi skirtingus matavimo vienetus. Skliausteliuose paryškinami matavimo vienetai, pagal kuriuos preliminariame etape paskirstoma „visa“. Matavimo vienetas, pagal kurį formuojamas rinkinys, išimamas iš skliaustų. Paskutinėje eilutėje rodomas galutinis rezultatas – rinkinio elementas. Kaip matote, jei aibei sudaryti naudojame vienetus, tai rezultatas nepriklauso nuo mūsų veiksmų eilės. Ir tai yra matematika, o ne šamanų šokiai su tamburinais. Šamanai gali „intuityviai“ pasiekti tą patį rezultatą, argumentuodami jį „akivaizdumu“, nes matavimo vienetai nėra įtraukti į jų „mokslinį“ arsenalą.

Matavimo vienetų pagalba labai lengva sulaužyti vieną arba sujungti kelis rinkinius į vieną superkomplektą. Pažvelkime atidžiau į šio proceso algebrą.

Prisiminti!

Pagal tris žinomus proporcijos narius visada galite rasti nežinomą (ketvirtąjį) narį.

išspręsti proporciją reiškia surasti visus jos narius. Išspręskime toliau pateiktą proporciją
(raskite „x“).

Norėdami rasti „x“, naudojame pagrindinę proporcijos savybę („kryžiaus“ taisyklę).

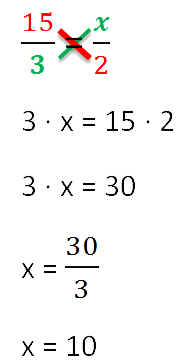
Dabar esame pasirengę išsiaiškinti, kaip išspręsti proporcijų problemas.

Proporcijų uždavinių sprendimas

Dažnai proporcijų užduotys glaudžiai susiję su procentais. Savo žinias apie procentus galite pagyvinti skiltyje „Pomėgiai“.

Užduotis

Iš lanko buvo paleista 50 šūvių. Pro taikinį praskriejo 5 strėlės. Nustatykite pataikymo procentą.

Pagal tradiciją mes akcentuojame svarbius ir skaitinius duomenis.

Atminkite, kad turime nustatyti įvykių procentą, o ne praleistų rodyklių procentą.

Todėl pirmiausia apskaičiuojame, kiek strėlių pataikė į taikinį. Tai padaryti nebus sunku.

50 − 5 = 45 (rodyklės) – pataikyti į taikinį.

Toliau, norėdami išspręsti problemą, padarysime lentelę, kurioje įvesime visus duomenis. Atminkite, kad priešais 100% lentelėje paprastai rašoma bendra kažko suma. Nežinomi procentai bus pažymėti raide x.

Norėdami teisingai įrašyti reikiamus duomenis į lentelę, atsiminkite paprastą taisyklę.

Dviejų santykių lygybė vadinama proporcija.

a :b =c :d. Tai yra proporcija. Skaityti: A taip taikoma b, Kaip c nurodo d. Skaičiai a Ir d paskambino ekstremalus proporcijos nariai ir skaičiai b Ir c – vidutinis proporcijos nariai.

Proporcijų pavyzdys: 1 2 : 3 = 16 : 4 . Tai yra dviejų santykių lygybė: 12:3= 4 ir 16:4= 4 . Jie skaito: dvylika yra prieš tris kaip šešiolika yra keturi. Čia 12 ir 4 yra kraštutiniai proporcijos nariai, o 3 ir 16 yra viduriniai proporcijos nariai.

Pagrindinė proporcijos savybė.

Proporcijos kraštutinių narių sandauga yra lygi jos vidurinių dalių sandaugai.

Dėl proporcijos a :b =c :d arba a/b=c/d pagrindinė savybė parašyta taip: a d \u003d b c .

Mūsų proporcijai 12 : 3 = 16 : 4 pagrindinė savybė bus parašyta taip: 12 4 = 3 16 . Pasirodo, teisinga lygybė: 48 \u003d 48 .

Norėdami rasti nežinomą kraštutinį proporcijos narį, turite padalyti vidutinių proporcijos narių sandaugą iš žinomo kraštutinio nario.

Pavyzdžiai.

1) x: 20 = 2: 5. Mes turime X Ir 5 yra kraštutiniai proporcijos nariai ir 20 Ir 2 - vidutinis.

Sprendimas.

x = (20 2):5- reikia padauginti vidurinius dėmenis ( 20 Ir 2 ) ir padalykite rezultatą iš žinomo kraštutinio termino (skaičiaus 5 );

x=40:5 yra vidurinių terminų produktas ( 40 ) padalinti iš žinomo kraštutinio termino ( 5 );

x = 8. Gavome norimą kraštutinį proporcijos terminą.

Nežinomo proporcijos nario radinį patogiau užrašyti naudojant paprastąją trupmeną. Štai kaip tada būtų parašytas mūsų svarstytas pavyzdys:

Norimas kraštutinis proporcijos terminas ( X) bus lygus vidurinių terminų sandaugai ( 20 Ir 2 ) padalintas iš žinomo kraštutinio termino ( 5 ).

Sumažiname trupmeną 5 (padalinti iš 5 X.

Daugiau tokių nežinomo kraštutinio proporcijos nario radimo pavyzdžių.

Norėdami rasti nežinomą vidurinį proporcijos narį, turite padalyti kraštutinių proporcijos narių sandaugą iš žinomo vidurinio nario.

Pavyzdžiai. Raskite nežinomą vidurinį proporcijos terminą.

5) 9: x = 3:14. Skaičius 3 yra žinomas vidutinis duotosios proporcijos terminas, skaičiai 9 Ir 14 yra kraštutinės proporcijos sąlygos.

Sprendimas.

x \u003d (9 14): 3 - padauginkite kraštutinius proporcijos narius ir padalykite rezultatą iš žinomo vidurinio proporcijos nario;

x= 136:3;

x=42.

Šio pavyzdžio sprendimas gali būti parašytas kitaip:

Reikalingas vidutinis proporcijos terminas ( X) bus lygus kraštutinių terminų sandaugai ( 9 Ir 14 ) padalintas iš žinomo vidurinio termino ( 3 ).

Sumažiname trupmeną 3 (padalinti iš 3 o trupmenos skaitiklis ir vardiklis). Vertės radimas X.

Jei pamiršote, kaip sumažinti paprastas trupmenas, pakartokite temą: ""

Daugiau tokių pavyzdžių, kaip rasti nežinomą vidutinį proporcijos narį.

Skyriai: Matematika

Pamokos tipas: Studijų ir pirminio naujų žinių įtvirtinimo pamoka.

Pamokos forma: Pamoka-tyrimas.

Pamokos tikslai:

aktyvinti mokinių pažintinę veiklą;
supažindinti mokinius su sąvokomis: proporcija, proporcijos nariai; teisingos ir neteisingos proporcijos;
supažindinti mokinius su pagrindine proporcijos savybe ir formuoti teisingos proporcijos nustatymo įgūdžius.

Įranga:

Maršruto lapuose nurodomi taškai, kuriuos galima gauti sprendžiant užduotis. Mokinys, vertindamas balus, atsižvelgia į savo sprendimo teisingumą, sprendimo greitį (savikontrolė ir abipusis patikrinimas pristatymo pagalba). Eilutėje „Papildomi taškai“ taškai suteikiami už atsakymą į papildomus klausimus, už pagalbą mokytojui organizuojant kitų mokinių testavimą, taip pat už pamokos temos „atspėjimą“.

Atvirutės supjaustomos ir vokuose išdalinamos mokiniams (po vieną voką ant stalo).

3. Magnetinės plokštės kortelės (1 pav., 2 pav., 3 pav.)

Pamokos metu šios kortelės iškabinamos ant magnetinės lentos.

4. Dėlionės (4 pav., 5 pav., 6 pav., 7 pav.).

Gimnazistų sudaryti rebusai (išskyrus rebusą „Proporcija“ – šis rebusas buvo paimtas iš pamokos, kurią FPI vedė mokytojas Kozak Tatjana Ivanovna, 20 vidurinė mokykla „Progress“, Amūro sritis), mokiniai yra pakvietė juos išspręsti po pamokos.

Pamokos techninė įranga – kompiuteris, projektorius pristatymui demonstruoti, ekranas. Kompiuterinis pristatymas Microsoft PowerPoint programoje (4 priedas).

I. Pamokos pradžios organizavimas

Sveiki! Patikrinkite, ar ant stalo yra dalomoji medžiaga, ar turite raudoną ir mėlyną pieštuką ir ar esate pasiruošę pamokai.

II. Pamokos pranešimų temos, tikslai ir uždaviniai.

Šiandien pamokoje toliau mokomės didelės matematikos kurso dalies. Baigėme studijuoti temą (kas? - "Požiūris"). Dabar pradedame tyrinėti naują šio skyriaus temą. Keletas pavyzdžių padės mums suprasti pamokos temą. Savo maršruto lapo tituliniame puslapyje turite užpildyti lentelę, spręsdami pavyzdžius žodžiu ir tada žinosite šios dienos pamokos temą. 1 SKAIDRĖ

Taigi, šios dienos pamokos tema Proporcija. 2 SKAIDRĖ

Žinodami pamokos temą, pabandykite sudaryti pamokos planą. Ko turėtum išmokti šiandien klasėje? Ką tu nori žinoti? Ko norite išmokti klasėje?

Sudarysime planą, kurį papildysime pamokos metu. (mokiniai įvardija pirmus du ir paskutinius du plano punktus, likusieji pildomi pamokos metu, nes „atrandamos“ naujos žinios; pamokos planas užrašomas lentoje)

- kartojimas (su požiūriu susiję klausimai)

Proporcijos apibrėžimas

PROPORCIJOS NARIAI

TEISINGOS IR NETEISINGOS PROporcijos

PAGRINDINĖS PROporcingumo SAVYBĖS

Taikymas matematikoje

Taikymas gyvenime

Paskutinius du punktus galėsime analizuoti tolesnėse pamokose, studijuodami temą.

III. Mokinių žinių atnaujinimas. Pasiruošimas aktyviai ugdomajai ir pažintinei veiklai pagrindiniame pamokos etape.

Su klasės draugu aptarkite klausimus, susijusius su tema „Požiūris“.

Kas pasiruošęs užduoti klausimus, susijusius su paskutine tema? (pūga) MP1

– Kas yra požiūris?

Kaip galite parašyti santykius?

Į kokius klausimus atsako požiūris?

Kaip parašyti dviejų skaičių santykį?

Kas gali pakeisti do ženklą?

Kodėl, jūsų manymu, kartojome šias sąvokas?

Jie mums padės mokantis naujos temos.

Paimkite vokus ir užmegzkite santykius AĮ b Ir cĮ d du keliai. (tik 4 santykiai) DARBAS DARUOSE.

MP2 Jūsų laukia keli santykiai. Raskite šių posakių reikšmę. 3 SKAIDRĖ

4: 0,5=
=
5: 10 =
=
8: 1 =
2,5: 5 =

Sugrupuokite ryšius pagal tam tikrą požymį ir padarykite atitinkamas lygybes.

IV. Naujų žinių įsisavinimas.

4: 0,5 = 8: 1 = 5: 10 = 2,5: 5

Kokiu pagrindu sugrupavote šiuos santykius?

– Jų vertės vienodos.

Gautos lygybės vadinamos proporcijomis.

Pagalvokite ir nustatykite proporcijas.

Užuomina – proporcija yra ... EKRANO ( lygybė)

Lygybė … KAS ( santykius)

Kiek santykių? ( du).

Kas įsitikinęs savo nuomone, surašykite apibrėžimą maršruto lape. MP3

Kas yra pasirengęs eiti prie lentos ir sudaryti proporcijos apibrėžimą? (3 priedas)

APIBRĖŽIMAS (magnetinėje lentoje): Proporcija yra dviejų santykių lygybė.

Pažvelkime į žodžio proporcijos interpretaciją rusų kalbos žodyne Ozhegov S.I. 4 SKAIDRĖ: „Proporcija – tai tam tikras dalių santykis tarpusavyje, proporcingumas. Matematikoje dviejų santykio lygybė.

Jūs taip pat suformulavote proporcijos apibrėžimą rusų kalbos žodyne!

Pagalvokite, su kokiu matematiniu terminu sutampa žodis „proporcija“? ( palūkanų). Kaip verčiamas terminas „procentas“? ( nuo šimto). Taigi „pro“ yra išverstas kaip „nuo“. Kokia žodžio dalis liko? (“ porcija“). Kur sutikote šį žodį? (virimo metu) Ką tai reiškia? ( dydis)

Žodis proporcija kilęs iš lotyniško žodžio proportio – proporcingumas. (etimologinis žodynas). 4 SKAIDRĖ

Naudodamiesi proporcijos apibrėžimu, parašykite proporcijas naudodami padalijimo ženklą ir trupmenos juostą. (DARBAS DARUOSE, vokeliai).

Maršruto lapuose surašykite proporciją raidėmis a, b, c, d. MP4

O dabar išsiaiškinsime, kaip vadinami proporciją sudarantys skaičiai.

Skaičiai a, b, c, d vadinami proporcijos nariais

Koks yra pirmasis ir paskutinis proporcijos terminas? ( a ir c)

O kas dažniausiai (gyvenime) vadinama pirmuoju ir paskutiniuoju? (ekstremalus)

Taigi terminai a ir b vadinami ...? (ekstremalus)

Kur yra terminai c ir d? (viduryje)

O kokie c ir d narių vardai? ( vidutinė)

Kurie nariai pažymėti raudonai? ( Į anksti)

spalva (Su retas) nariai.

viduriniai terminai

Grįžkime prie pamokos plano – ar turite ką papildyti? (kraštutiniai ir viduriniai proporcijos nariai)

V. Pirminis žinių įtvirtinimas

MP5 Užpildykite lentelę:

Kokią išvadą galima padaryti? Įrašykite išvestį į maršrutą. ( Proporcingai kraštutinių dėmenų sandauga yra lygi vidurinių dalių sandaugai)8 SKAIDRĖ

MP6 Štai penkios lygybės. Ar visos proporcijos?

Pabrėžkite proporcijas.

= ; 7 + 11 = 36: 2; 72: 9 = 16: 2; = 20: 4; 5 40 = 100 2

7 SKAIDRĖ Atsistokite, kas baigė.

Ar visi tikri, kad čia yra trys proporcijos? Iš tiesų, paskutinėje lygybėje kraštutinių terminų sandauga nėra lygi vidurinių sandaugai. Grįžkime prie proporcijos apibrėžimo ( Proporcija – dviejų santykių lygybė). Ar trečioji lygybė yra dviejų santykių lygybė? (yra). Pagal apibrėžimą, ar tai proporcija? (Taip). Ar kraštutinių dėmenų sandauga lygi viduriniųjų narių sandaugai? (Ne). Taigi tai proporcija...? (neteisingai).Ši proporcija vadinama neteisinga. Taigi, yra neteisingos proporcijos ir ...? (Ištikimas). Suformuluokite pagrindinę proporcijos savybę, naudodamiesi įgytomis žiniomis. (Teisinga proporcija kraštutinių dėmenų sandauga yra lygi vidurinių sandaugai).

VI. Žinių įtvirtinimas.

Užpildyk lentelę.

Teisinga proporcija Neteisinga proporcija

= = 20: 4

Kaip kitaip galite nustatyti teisingą ar netinkamą proporciją? (raskite santykių vertę)

Ateityje kalbėsime apie teisingas proporcijas.

Grįžkime prie pamokos plano. Ką galima pridėti? (teisingos ir neteisingos proporcijos)

MP7 Naudodami raides B ir H pažymėkite teisingas ir neteisingas proporcijas.

= 1: 0,5 = 4,8: 2,4
7,5: 5 = 2: 3 =
10: 3 = 3 : 1 5:x = 20:4x

VII. Apibendrinimas ir sisteminimas.

MP8 Naudodami pagrindinę proporcijos savybę, sudarykite teisingą proporciją iš šių skaičių: 4, 5, 12, 15. Kiek teisingų proporcijų galite padaryti?

VIII. Žinių kontrolė ir savikontrolė

MP9 matematikos diktantas

Užrašykite proporciją: Skaičius 18 yra susijęs su 4, o 27 yra susijęs su 6.
Užrašykite proporciją: santykis nuo trijų iki penkių yra lygus santykiui nuo dviejų iki septynių.
Užrašykite vidutines proporcijos dalis: 1,5: 2 \u003d 4,5: 6
Užrašykite kraštutinius proporcijos narius: 2/1,9 = 3/2,8
Ar 3 dalyje nurodyta proporcija teisinga?
Ar teisinga proporcija 4 punkte?
Ar teisingas teiginys: lygties šaknis yra 20/5 \u003d x / 0,5 skaičius 2
Ar teisingas šis teiginys: Proporcijai sudaryti galima naudoti bet kokius keturis natūraliuosius skaičius?

10 SKAIDRĖ. Tarpusavio vertinimas

IX. Apibendrinant pamoką.

Žiūrėkite pamokos planą.

Ko šiandien išmokote klasėje? (kas yra proporcija, iš ko susideda proporcija, proporcijos teisingos ir neteisingos, pagrindinė proporcijos savybė, ...)

Ko šiandien išmokote klasėje? (nustatykite kraštutinį ir vidurinį proporcijos narius, išsiaiškinkite, ar proporcija teisinga, ar neteisinga, ...)

Kokius kitus klausimus galima užduoti pamokos pabaigoje?

-Kiek teisingų proporcijų galima padaryti iš šios teisingos proporcijos?

Kaip nustatyti, ar proporcija teisinga, ar neteisinga?

Prisiminkime paskutinę matematinio diktanto užduotį.

Proporcijai sudaryti gali būti naudojami bet kokie keturi natūralieji skaičiai. Teisingas atsakymas yra TAIP. Galite sudaryti proporciją, tačiau ji nebūtinai bus teisinga.

Iš frazės " Proporcijai sudaryti gali būti naudojami bet kokie keturi natūralieji skaičiai. Pašalinkite vieną žodį, kad šis teiginys būtų neteisingas. (natūralus). Kodėl? (Skaičius 0 negali būti proporcijos narys). Proporcijai sudaryti galima naudoti bet kokius keturis skaičius

Šioje frazėje Proporcijai sudaryti gali būti naudojami bet kokie keturi natūralieji skaičiai.įterpkite vieną žodį, kad teiginys būtų neteisingas (tiesa). Iš bet kurių keturių natūraliųjų skaičių galite sudaryti teisingą proporciją.

Apskaičiuokite per pamoką surinktų taškų skaičių ir skirkite pažymį.

X. Informacija apie namų darbus ir instrukcija, kaip juos atlikti

Matematika - 6, Vilenkin N.Ya. ir kt., 6-asis leidimas

P.21, Nr. 760, 781, 782, 783 (a)

Dviejų skaičių santykis

1 apibrėžimas

Dviejų skaičių santykis yra jų privatus.

1 pavyzdys

Santykis nuo 18 USD iki 3 USD gali būti parašytas taip:

18 USD\div 3=\frac(18)(3)=6 USD.

Santykis nuo 5 USD iki 15 USD gali būti parašytas taip:

$5\div 15=\frac(5)(15)=\frac(1)(3)$.

Naudojant dviejų skaičių santykis gali būti parodyta:

kiek kartų vienas skaičius didesnis už kitą;
kokią dalį atstoja vienas skaičius iš kito.

Sudarant dviejų skaičių santykį trupmenos vardiklyje, užrašykite skaičių, su kuriuo lyginama.

Dažniausiai toks skaičius seka po žodžių „palyginti su...“ arba prielinksnio „į ...“.

Prisiminkite pagrindinę trupmenos savybę ir pritaikykite ją ryšiui:

1 pastaba

Abu santykio narius daugindami arba padalydami iš to paties skaičiaus, išskyrus nulį, gauname santykį, lygų pradiniam.

Apsvarstykite pavyzdį, iliustruojantį dviejų skaičių santykio sąvokos vartojimą.

2 pavyzdys

Kritulių kiekis praėjusį mėnesį buvo $195 $ mm, o šį mėnesį - $ 780 $ mm. Kiek kritulių iškrito šį mėnesį, palyginti su praėjusiu mėnesiu?

Sprendimas.

Sudarykite einamojo mėnesio kritulių kiekio ir praėjusio mėnesio kritulių kiekio santykį:

$\frac(780)(195)=\frac(780\div 5)(195\div 5)=\frac(156\div 3)(39\div 3)=\frac(52)(13)=4 $.

Atsakymas: kritulių kiekis einamąjį mėnesį yra $4$ kartus didesnis nei praėjusį mėnesį.

3 pavyzdys

Raskite, kiek kartų skaičius $1 \frac(1)(2)$ yra skaičiuje $13 \frac(1)(2)$.

Sprendimas.

13 USD \frac(1)(2)\div 1 \frac(1)(2)=\frac(27)(2)\div \frac(3)(2)=\frac(27)(2) \cdot \frac(2)(3)=\frac(27)(3)=9$.

Atsakymas: $9 $ kartus.

Proporcingumo samprata

2 apibrėžimas

Proporcija vadinama dviejų santykių lygybe:

$a\div b=c\div d$

$\frac(a)(b)=\frac(c)(d)$.

4 pavyzdys

$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,

$\frac(8)(2)=\frac(36)(9)$, $\frac(10)(40)=\frac(9)(36)$, $\frac(15)(75)= \frac(1)(5)$.

Santykyje $\frac(a)(b)=\frac(c)(d)$ (arba $a:b = c\div d$) vadinami skaičiai a ir d ekstremalūs nariai proporcijos, o skaičiai $b$ ir $c$ yra viduriniai nariai proporcijas.

Teisingą proporciją galima konvertuoti taip:

2 pastaba

Teisingos proporcijos kraštutinių narių sandauga yra lygi vidurinių narių sandaugai:

$a \cdot d=b \cdot c$.

Šis teiginys yra pagrindinė proporcijos savybė.

Ir atvirkščiai:

3 pastaba

Jei proporcijos kraštutinių narių sandauga yra lygi jos vidurinių dalių sandaugai, tada proporcija yra teisinga.

4 pastaba

Jei viduriniai ar kraštutiniai terminai yra pertvarkyti teisinga proporcija, tada proporcijos, kurios bus gautos, taip pat bus teisingos.

5 pavyzdys

6 USD\div 3=18\div 9$, 15$\div 5=27\div 9$, 2$\div 4=12\div 24$,

$\frac(2)(8)=\frac(9)(36)$, $\frac(40)(10)=\frac(36)(9)$, $\frac(75)(15)= \frac(5)(1)$.

Naudojant šią savybę, nesunku rasti nežinomą terminą iš proporcijos, jei žinomi kiti trys:

$a=\frac(b \cdot c)(d)$; $b=\frac(a \cdot d)(c)$; $c=\frac(a \cdot d)(b)$; $d=\frac(b \cdot c)(a)$.

6 pavyzdys

$\frac(6)(a)=\frac(16)(8)$;

6 USD \cdot 8=16 \cdot a$;

16 USD \cdot a=6 \cdot 8$;

16 USD \cdot a=48 USD;

$a=\frac(48)(16)$;

7 pavyzdys

$\frac(a)(21)=\frac(8)(24)$;

$a \cdot 24=21 \cdot 8$;

$a \cdot 24=168$;

$a=\frac(168)(24)$;

3 USD sodininkas – 108 USD medžiai;

$x$ sodininkai – $252$ medis.

Padarykime proporciją:

$\frac(3)(x)=\frac(108)(252)$.

Naudokime taisyklę nežinomam proporcijos nariui rasti:

$b=\frac(a \cdot d)(c)$;

$x=\frac(3 \cdot 252)(108)$;

$x=\frac(252)(36)$;

Atsakymas: Sodininkams nugenėti 252 USD kainuojančius medžius prireiks 7 USD.

Dažniausiai proporcijos savybės praktikoje naudojamos matematiniuose skaičiavimuose tais atvejais, kai reikia apskaičiuoti nežinomo proporcijos nario vertę, jei žinomos kitų trijų narių reikšmės.