Cum să faci proporția potrivită. Cum se calculează proporția. Cum să rezolvi o problemă folosind proporția
Mai simplu spus, acestea sunt legume fierte în apă după o rețetă specială. Voi lua în considerare două componente inițiale (salata de legume și apă) și rezultatul final - borș. Geometric, acesta poate fi reprezentat ca un dreptunghi în care o parte desemnează salată verde, cealaltă parte desemnează apă. Suma acestor două laturi va desemna borș. Diagonala și aria unui astfel de dreptunghi „borș” sunt concepte pur matematice și nu sunt niciodată folosite în rețetele de borș.
Cum se transformă salata verde și apa în borș în ceea ce privește matematica? Cum se poate transforma suma a două segmente în trigonometrie? Pentru a înțelege acest lucru, avem nevoie de funcții unghiulare liniare.
Nu veți găsi nimic despre funcțiile unghiulare liniare în manualele de matematică. Dar fără ele nu poate exista matematică. Legile matematicii, ca și legile naturii, funcționează indiferent dacă știm că există sau nu.
Funcțiile unghiulare liniare sunt legile adunării. Vedeți cum algebra se transformă în geometrie și geometria se transformă în trigonometrie.
Este posibil să faci fără funcții unghiulare liniare? Poți, pentru că matematicienii încă se descurcă fără ele. Smecheria matematicienilor constă în faptul că ei ne vorbesc întotdeauna doar despre acele probleme pe care ei înșiși le pot rezolva și niciodată nu ne vorbesc despre acele probleme pe care nu le pot rezolva. Vedea. Dacă știm rezultatul adunării și al unui termen, folosim scăderea pentru a găsi celălalt termen. Toate. Nu cunoaștem alte probleme și nu suntem capabili să le rezolvăm. Ce să facem dacă știm doar rezultatul adunării și nu știm ambii termeni? În acest caz, rezultatul adunării trebuie descompus în doi termeni folosind funcții unghiulare liniare. Mai mult, noi înșine alegem ce poate fi un termen, iar funcțiile unghiulare liniare arată care ar trebui să fie al doilea termen pentru ca rezultatul adunării să fie exact ceea ce avem nevoie. Pot exista un număr infinit de astfel de perechi de termeni. În viața de zi cu zi, ne descurcăm foarte bine fără a descompune suma; scăderea ne este suficientă. Dar în studiile științifice ale legilor naturii, extinderea sumei în termeni poate fi foarte utilă.
O altă lege a adunării despre care matematicienii nu le place să vorbească (un alt truc de-al lor) cere ca termenii să aibă aceeași unitate de măsură. Pentru salată verde, apă și borș, acestea pot fi unități de greutate, volum, cost sau unitate de măsură.
Figura arată două niveluri de diferență pentru matematică. Primul nivel este diferențele în domeniul numerelor, care sunt indicate A, b, c. Asta fac matematicienii. Al doilea nivel este diferențele în zona unităților de măsură, care sunt afișate între paranteze drepte și sunt indicate prin litera U. Asta fac fizicienii. Putem înțelege al treilea nivel - diferențele în domeniul de aplicare al obiectelor descrise. Obiecte diferite pot avea același număr de aceleași unități de măsură. Cât de important este acest lucru, putem vedea pe exemplul trigonometriei borș. Dacă adăugăm indicele la aceeași notație pentru unitățile de măsură ale diferitelor obiecte, putem spune exact ce mărime matematică descrie un anumit obiect și cum se modifică acesta în timp sau în legătură cu acțiunile noastre. scrisoare W Voi marca apa cu litera S Voi marca salata cu litera B- borș. Iată cum ar arăta funcțiile unghiului liniar pentru borș.
Dacă luăm o parte din apă și o parte din salată, împreună se vor transforma într-o porție de borș. Aici vă sugerez să faceți o mică pauză de la borș și să vă amintiți de copilăria voastră îndepărtată. Îți amintești cum am fost învățați să punem iepurași și rațe împreună? A fost necesar să se afle câte animale vor ieși. Atunci ce am fost învățați să facem? Am fost învățați să separăm unitățile de numere și să adunăm numere. Da, orice număr poate fi adăugat oricărui alt număr. Aceasta este o cale directă către autismul matematicii moderne - nu înțelegem ce, nu este clar de ce și înțelegem foarte puțin cum se raportează acest lucru la realitate, din cauza celor trei niveluri de diferență, matematicienii operează doar pe unul. Va fi mai corect să înveți cum să treci de la o unitate de măsură la alta.
Și iepurașii, rațele și animalele mici pot fi numărate în bucăți. O unitate de măsură comună pentru diferite obiecte ne permite să le adunăm. Aceasta este o versiune a problemei pentru copii. Să ne uităm la o problemă similară pentru adulți. Ce obții când adaugi iepurași și bani? Există două soluții posibile aici.
Prima varianta. Determinăm valoarea de piață a iepurașilor și o adăugăm la numerarul disponibil. Am obținut valoarea totală a bogăției noastre în termeni de bani.
A doua varianta. Puteți adăuga numărul de iepurași la numărul de bancnote pe care le avem. Vom obține cantitatea de bunuri mobile în bucăți.
După cum puteți vedea, aceeași lege de adunare vă permite să obțineți rezultate diferite. Totul depinde de exact ce vrem să știm.
Dar să revenim la borșul nostru. Acum putem vedea ce se va întâmpla cu diferite valori ale unghiului funcțiilor unghiului liniar.
Unghiul este zero. Avem salată, dar fără apă. Nu putem găti borș. Cantitatea de borș este, de asemenea, zero. Acest lucru nu înseamnă deloc că zero borș este egal cu zero apă. Zero borș poate fi și la zero salată (unghi drept).
Pentru mine personal, aceasta este principala dovadă matematică a faptului că . Zero nu schimbă numărul atunci când este adăugat. Acest lucru se datorează faptului că adăugarea în sine este imposibilă dacă există un singur termen și lipsește al doilea termen. Vă puteți raporta la asta după cum doriți, dar amintiți-vă - toate operațiile matematice cu zero au fost inventate de matematicieni înșiși, așa că renunțați la logica și înghesuiți prostește definițiile inventate de matematicieni: „împărțirea cu zero este imposibilă”, „orice număr înmulțit cu zero”. este egal cu zero”, „în spatele punctului zero” și alte prostii. Este suficient să vă amintiți o dată că zero nu este un număr și nu veți avea niciodată o întrebare dacă zero este un număr natural sau nu, deoarece o astfel de întrebare pierde în general orice semnificație: cum se poate considera un număr ceea ce nu este un număr . Este ca și cum ai întreba ce culoare să-i atribui o culoare invizibilă. A adăuga zero la un număr este ca și cum ai picta cu vopsea care nu există. Au fluturat o pensulă uscată și spun tuturor că „am pictat”. Dar mă abatem puțin.
Unghiul este mai mare decât zero, dar mai mic de patruzeci și cinci de grade. Avem multă salată verde, dar puțină apă. Drept urmare, obținem un borș gros.
Unghiul este de patruzeci și cinci de grade. Avem cantități egale de apă și salată verde. Acesta este borșul perfect (fie ca bucătarii să mă ierte, e doar matematică).
Unghiul este mai mare de patruzeci și cinci de grade, dar mai mic de nouăzeci de grade. Avem multă apă și puțină salată verde. Luați borș lichid.
Unghi drept. Avem apă. Au rămas doar amintiri despre salată, în timp ce continuăm să măsurăm unghiul de la linia care a marcat cândva salata. Nu putem găti borș. Cantitatea de borș este zero. În acest caz, ține-te și bea apă cât este disponibilă)))
Aici. Ceva de genul. Pot spune și alte povești aici care vor fi mai mult decât potrivite aici.
Cei doi prieteni aveau cotele lor în afacerea comună. După uciderea unuia dintre ei, totul a mers către celălalt.
Apariția matematicii pe planeta noastră.
Toate aceste povești sunt spuse în limbajul matematicii folosind funcții unghiulare liniare. Altă dată vă voi arăta locul real al acestor funcții în structura matematicii. Între timp, să revenim la trigonometria borșului și să luăm în considerare proiecțiile.
Sâmbătă, 26 octombrie 2019
miercuri, 7 august 2019
Încheind conversația despre , trebuie să luăm în considerare un set infinit. A dat prin faptul că conceptul de „infinit” acționează asupra matematicienilor, ca un boa constrictor asupra unui iepure. Oroarea tremurătoare a infinitului îi privează pe matematicieni de bunul simț. Iată un exemplu:
Se află sursa originală. Alfa denotă un număr real. Semnul egal din expresiile de mai sus indică faptul că dacă adăugați un număr sau un infinit la infinit, nimic nu se va schimba, rezultatul va fi același infinit. Dacă luăm ca exemplu un set infinit de numere naturale, atunci exemplele luate în considerare pot fi reprezentate după cum urmează:
Pentru a-și demonstra vizual cazul, matematicienii au venit cu multe metode diferite. Personal, privesc toate aceste metode ca pe dansurile șamanilor cu tamburine. În esență, toate se rezumă la faptul că fie unele camere nu sunt ocupate și se stabilesc noi oaspeți în ele, fie că unii dintre vizitatori sunt aruncați pe coridor pentru a face loc oaspeților (foarte uman). Mi-am prezentat punctul de vedere asupra unor astfel de decizii sub forma unei povești fantastice despre Blonda. Pe ce se bazează raționamentul meu? Mutarea unui număr infinit de vizitatori durează o perioadă infinită de timp. După ce am eliberat prima cameră de oaspeți, unul dintre vizitatori va merge mereu de-a lungul coridorului din camera lui în următoarea până la sfârșitul timpului. Desigur, factorul timp poate fi ignorat în mod prostesc, dar acesta va fi deja din categoria „legea nu este scrisă pentru proști”. Totul depinde de ceea ce facem: adaptăm realitatea la teoriile matematice sau invers.
Ce este un „hotel infinit”? Un han infinit este un han care are întotdeauna orice număr de locuri libere, indiferent de câte camere sunt ocupate. Dacă toate camerele din holul nesfârșit „pentru vizitatori” sunt ocupate, există un alt hol nesfârșit cu camere pentru „oaspeți”. Vor exista un număr infinit de astfel de coridoare. În același timp, „hotelul infinit” are un număr infinit de etaje într-un număr infinit de clădiri pe un număr infinit de planete într-un număr infinit de universuri create de un număr infinit de Zei. Matematicienii, pe de altă parte, nu sunt capabili să se îndepărteze de problemele banale de zi cu zi: Dumnezeu-Allah-Buddha este întotdeauna unul singur, hotelul este unul, coridorul este doar unul. Așadar, matematicienii încearcă să jongleze cu numerele de serie ale camerelor de hotel, convingându-ne că este posibil să „împingem cei neîmpinși”.
Vă voi demonstra logica raționamentului meu folosind exemplul unui set infinit de numere naturale. Mai întâi trebuie să răspundeți la o întrebare foarte simplă: câte seturi de numere naturale există - unul sau mai multe? Nu există un răspuns corect la această întrebare, deoarece noi înșine am inventat numerele, nu există numere în Natură. Da, Natura știe să numere perfect, dar pentru asta folosește alte instrumente matematice care nu ne sunt familiare. După cum crede Natura, vă voi spune altă dată. Din moment ce am inventat numerele, noi înșine vom decide câte seturi de numere naturale există. Luați în considerare ambele opțiuni, așa cum se cuvine unui adevărat om de știință.
Opțiunea unu. „Să ni se dea” un singur set de numere naturale, care se află senin pe un raft. Luăm acest set de pe raft. Gata, nu au mai rămas alte numere naturale pe raft și nu există unde să le duci. Nu putem adăuga unul la acest set, deoarece îl avem deja. Dacă vrei cu adevărat? Nici o problemă. Putem lua o unitate din setul pe care l-am luat deja și o putem întoarce la raft. După aceea, putem lua o unitate de pe raft și o putem adăuga la ce ne-a mai rămas. Ca rezultat, obținem din nou un set infinit de numere naturale. Puteți scrie toate manipulările noastre astfel:
Am notat operațiile în notație algebrică și în notație în teoria mulțimilor, enumerând în detaliu elementele mulțimii. Indicele indică faptul că avem unul și singurul set de numere naturale. Se dovedește că mulțimea numerelor naturale va rămâne neschimbată numai dacă din el se scade unul și se adaugă același.
Varianta a doua. Avem multe seturi infinite diferite de numere naturale pe raft. Subliniez - DIFERITE, în ciuda faptului că practic nu se pot distinge. Luăm unul dintre aceste seturi. Apoi luăm unul dintr-un alt set de numere naturale și îl adăugăm la setul pe care l-am luat deja. Putem adăuga chiar două seturi de numere naturale. Iată ce primim:
Indicele „unu” și „doi” indică faptul că aceste elemente aparțineau unor seturi diferite. Da, dacă adăugați unul la un set infinit, rezultatul va fi și un set infinit, dar nu va fi același cu setul original. Dacă la o mulțime infinită se adaugă o altă mulțime infinită, rezultatul este o nouă mulțime infinită constând din elementele primelor două mulțimi.
Setul de numere naturale este folosit pentru numărare în același mod ca o riglă pentru măsurători. Acum imaginați-vă că ați adăugat un centimetru la riglă. Aceasta va fi deja o linie diferită, nu egală cu originalul.
Puteți să acceptați sau să nu acceptați raționamentul meu - aceasta este treaba voastră. Dar dacă te confrunți vreodată cu probleme matematice, gândește-te dacă te afli pe calea raționamentului fals, călcat de generații de matematicieni. La urma urmei, orele de matematică, în primul rând, formează în noi un stereotip stabil de gândire și abia apoi ne adaugă abilități mentale (sau invers, ne privează de gândirea liberă).
pozg.ru
Duminică, 4 august 2019
Scriam un postscript la un articol despre și am văzut acest text minunat pe Wikipedia:
Citim: „... baza teoretică bogată a matematicii babiloniene nu avea un caracter holistic și s-a redus la un set de tehnici disparate, lipsite de un sistem comun și de o bază de dovezi”.
Wow! Cât de deștepți suntem și cât de bine putem vedea neajunsurile celorlalți. Este slab pentru noi să privim matematica modernă în același context? Parafrazând ușor textul de mai sus, personal am obținut următoarele:
Baza teoretică bogată a matematicii moderne nu are un caracter holistic și se reduce la un set de secțiuni disparate, lipsite de un sistem comun și bază de dovezi.
Nu voi merge departe pentru a-mi confirma cuvintele - are un limbaj și convenții care sunt diferite de limbajul și convențiile multor alte ramuri ale matematicii. Aceleași nume în diferite ramuri ale matematicii pot avea semnificații diferite. Vreau să dedic un întreg ciclu de publicații celor mai evidente gafe ale matematicii moderne. Pe curând.
Sâmbătă, 3 august 2019
Cum se împarte un set în subseturi? Pentru a face acest lucru, trebuie să introduceți o nouă unitate de măsură, care este prezentă în unele dintre elementele setului selectat. Luați în considerare un exemplu.
Să avem multe A format din patru persoane. Acest set este format pe baza de „oameni” Să desemnăm elementele acestui set prin scrisoare A, indicele cu un număr va indica numărul ordinal al fiecărei persoane din acest set. Să introducem o nouă unitate de măsură „caracteristica sexuală” și să o notăm cu literă b. Deoarece caracteristicile sexuale sunt inerente tuturor oamenilor, înmulțim fiecare element al setului A pe gen b. Observați că setul nostru de „oameni” a devenit acum setul de „oameni cu gen”. După aceea, putem împărți caracteristicile sexuale în masculin bmși de femei bw caracteristicile de gen. Acum putem aplica un filtru matematic: selectăm una dintre aceste caracteristici sexuale, indiferent care este bărbat sau femeie. Dacă este prezent la o persoană, atunci îl înmulțim cu unul, dacă nu există un astfel de semn, îl înmulțim cu zero. Și apoi aplicăm matematica obișnuită a școlii. Vezi ce sa întâmplat.
După înmulțire, reduceri și rearanjamente, am obținut două submulțimi: submulțimea masculină bmși un subgrup de femei bw. Aproximativ în același mod în care matematicienii raționează atunci când aplică teoria mulțimilor în practică. Dar ei nu ne lasă să intrăm în detalii, ci ne oferă rezultatul final - „mulți oameni sunt formați dintr-un subset de bărbați și un subset de femei”. Desigur, este posibil să aveți o întrebare, cât de corect aplicați matematica în transformările de mai sus? Îndrăznesc să vă asigur că de fapt transformările sunt făcute corect, este suficient să cunoașteți justificarea matematică a aritmeticii, algebrei booleene și a altor secțiuni ale matematicii. Ce este? Altă dată vă voi povesti despre asta.
În ceea ce privește superseturile, este posibil să combinați două mulțimi într-un singur superset, alegând o unitate de măsură care este prezentă în elementele acestor două mulțimi.
După cum puteți vedea, unitățile de măsură și matematica obișnuită fac ca teoria seturilor să devină un lucru din trecut. Un semn că totul nu este în regulă cu teoria mulțimilor este că matematicienii au venit cu propriul lor limbaj și notație pentru teoria mulțimilor. Matematicienii au făcut ceea ce şamanii au făcut cândva. Doar șamanii știu să-și aplice „corect” „cunoștințele”. Această „cunoaștere” ne-o învață.
În cele din urmă, vreau să vă arăt cum manipulează matematicienii.
luni, 7 ianuarie 2019
În secolul al V-lea î.Hr., filosoful antic grec Zenon din Elea și-a formulat celebrele aporii, dintre care cea mai cunoscută este aporia „Achile și broasca țestoasă”. Iată cum sună:
Să presupunem că Ahile aleargă de zece ori mai repede decât țestoasa și este la o mie de pași în spatele ei. În timpul în care Ahile parcurge această distanță, țestoasa se târăște o sută de pași în aceeași direcție. Când Ahile a alergat o sută de pași, țestoasa se va târa încă zece pași și așa mai departe. Procesul va continua la nesfârșit, Ahile nu va ajunge niciodată din urmă cu broasca țestoasă.
Acest raționament a devenit un șoc logic pentru toate generațiile următoare. Aristotel, Diogene, Kant, Hegel, Gilbert... Toți, într-un fel sau altul, au considerat aporii lui Zenon. Șocul a fost atât de puternic încât " ... discuțiile continuă în prezent, comunitatea științifică nu a reușit încă să ajungă la o opinie comună cu privire la esența paradoxurilor... în studiul problemei au fost implicate analiza matematică, teoria mulțimilor, noi abordări fizice și filozofice ; niciunul dintre ele nu a devenit o soluție universal acceptată la problemă...„[Wikipedia,” Aporii lui Zeno „]. Toată lumea înțelege că sunt păcăliți, dar nimeni nu înțelege ce este înșelăciunea.
Din punctul de vedere al matematicii, Zenon în aporia sa a demonstrat clar trecerea de la valoare la. Această tranziție implică aplicarea în loc de constante. Din câte am înțeles, aparatul matematic pentru aplicarea unităților de măsură variabile fie nu a fost încă dezvoltat, fie nu a fost aplicat aporiei lui Zenon. Aplicarea logicii noastre obișnuite ne duce într-o capcană. Noi, prin inerția gândirii, aplicăm reciprocului unități constante de timp. Din punct de vedere fizic, aceasta pare o încetinire a timpului până când se oprește complet în momentul în care Ahile ajunge din urmă cu țestoasa. Dacă timpul se oprește, Ahile nu mai poate depăși țestoasa.
Dacă întoarcem logica cu care suntem obișnuiți, totul cade la locul său. Ahile aleargă cu o viteză constantă. Fiecare segment ulterior al traseului său este de zece ori mai scurt decât cel anterior. În consecință, timpul petrecut pentru depășirea acestuia este de zece ori mai mic decât cel anterior. Dacă aplicăm conceptul de „infinit” în această situație, atunci ar fi corect să spunem „Achile va depăși infinit rapid broasca țestoasă”.
Cum să eviți această capcană logică? Rămâneți în unități constante de timp și nu treceți la valori reciproce. În limba lui Zeno, arată astfel:
În timpul necesar lui Ahile să alerge o mie de pași, țestoasa se târăște o sută de pași în aceeași direcție. În următorul interval de timp, egal cu primul, Ahile va alerga încă o mie de pași, iar țestoasa se va târa o sută de pași. Acum Ahile este cu opt sute de pași înaintea țestoasei.
Această abordare descrie în mod adecvat realitatea fără niciun paradox logic. Dar aceasta nu este o soluție completă a problemei. Afirmația lui Einstein despre insurmontabilitatea vitezei luminii este foarte asemănătoare cu aporia lui Zeno „Achile și broasca țestoasă”. Încă trebuie să studiem, să regândim și să rezolvăm această problemă. Iar soluția trebuie căutată nu în număr infinit de mare, ci în unități de măsură.
O altă aporie interesantă a lui Zeno spune despre o săgeată zburătoare:
O săgeată zburătoare este nemișcată, deoarece în fiecare moment de timp este în repaus și, deoarece este în repaus în fiecare moment de timp, este întotdeauna în repaus.
În această aporie, paradoxul logic este depășit foarte simplu - este suficient să clarificăm că în fiecare moment de timp săgeata zburătoare se odihnește în diferite puncte din spațiu, care, de fapt, este mișcare. Mai este un punct de remarcat aici. Dintr-o fotografie a unei mașini pe șosea, este imposibil să se determine nici faptul mișcării acesteia, nici distanța până la ea. Pentru a determina fapta mișcării mașinii, sunt necesare două fotografii realizate din același punct în momente diferite în timp, dar nu pot fi folosite pentru a determina distanța. Pentru a determina distanța până la mașină, aveți nevoie de două fotografii realizate din diferite puncte din spațiu în același timp, dar nu puteți determina faptul deplasării din ele (în mod firesc, aveți nevoie de date suplimentare pentru calcule, trigonometria vă va ajuta). Ceea ce vreau să subliniez în special este că două puncte în timp și două puncte în spațiu sunt două lucruri diferite care nu trebuie confundate, deoarece oferă oportunități diferite de explorare.
Voi arăta procesul cu un exemplu. Selectăm „solid roșu într-un coș” - acesta este „întregul nostru”. În același timp, vedem că aceste lucruri sunt cu arc și există fără arc. După aceea, selectăm o parte din „întreg” și formăm un set „cu un arc”. Așa se hrănește șamanii legându-și teoria seturilor de realitate.
Acum hai să facem un mic truc. Să luăm „solid într-un coș cu fundă” și să unim aceste „întregi” după culoare, selectând elemente roșii. Avem mult „roșu”. Acum o întrebare dificilă: seturile primite „cu fundă” și „roșu” sunt același set sau două seturi diferite? Doar șamanii știu răspunsul. Mai exact, ei înșiși nu știu nimic, dar așa cum spun ei, așa să fie.
Acest exemplu simplu arată că teoria seturilor este complet inutilă când vine vorba de realitate. Care este secretul? Am format un set de „coșuri roșii solide cu fundă”. Formarea a avut loc după patru unități de măsură diferite: culoare (roșu), rezistență (solid), rugozitate (în coș), decorațiuni (cu fundă). Doar un set de unități de măsură face posibilă descrierea adecvată a obiectelor reale în limbajul matematicii. Iată cum arată.
Litera „a” cu indici diferiți indică unități de măsură diferite. În paranteze sunt evidențiate unitățile de măsură, conform cărora „întregul” este alocat în etapa preliminară. Unitatea de măsură, conform căreia se formează setul, este scoasă din paranteze. Ultima linie arată rezultatul final - un element al setului. După cum puteți vedea, dacă folosim unități pentru a forma un set, atunci rezultatul nu depinde de ordinea acțiunilor noastre. Și aceasta este matematică, și nu dansurile șamanilor cu tamburine. Șamanii pot ajunge „intuitiv” la același rezultat, argumentând cu „evident”, deoarece unitățile de măsură nu sunt incluse în arsenalul lor „științific”.
Cu ajutorul unităților de măsură, este foarte ușor să spargi unul sau să combinați mai multe seturi într-un singur superset. Să aruncăm o privire mai atentă asupra algebrei acestui proces.
Tine minte!
Prin trei membri cunoscuți ai proporției, puteți găsi întotdeauna (al patrulea) membru necunoscut.
rezolva proportieînseamnă să-i găsești toți membrii. Să rezolvăm proporția de mai jos
(găsiți „x”).

Pentru a găsi „x”, folosim principala proprietate a proporției (regula „crucii”).
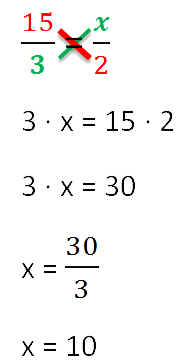
Acum suntem gata să ne dăm seama cum să rezolvăm problemele de proporție.
Rezolvarea problemelor de proporții
De multe ori sarcini de proporție strâns legată de procente. Puteți să vă îmbunătățiți cunoștințele despre procente în secțiunea „Dobânzi”.
Sarcină
Din prova au fost trase 50 de focuri. 5 săgeți au zburat pe lângă țintă. Determinați procentul de accesare.
Prin tradiție, punem accent pe datele importante și numerice în problemă.
Rețineți că trebuie să stabilim procentul de accesări, nu procentul de săgeți care ratează.
Prin urmare, mai întâi calculăm câte săgeți au lovit ținta. Nu va fi greu să faci asta.
- 50 − 5 = 45 (săgeți) - loviți ținta.
În continuare, pentru a rezolva problema, vom face un tabel în care vom introduce toate datele. Amintiți-vă că opusul 100% în tabel este de obicei scrisă suma totală a ceva. Procentele necunoscute vor fi notate cu litera x.
Pentru a înregistra corect datele necesare în tabel, amintiți-vă o regulă simplă.
Egalitatea a două rapoarte se numește proporție.
a :b =c :d. Aceasta este proporția. Citit: A deci se aplica la b, Cum c se refera la d. Numerele AȘi d numit extrem membrii proporției și numerele bȘi c – in medie membri ai proporţiei.
Exemplu de proporție: 1 2 : 3 = 16 : 4 . Aceasta este egalitatea a două rapoarte: 12:3= 4 și 16:4= 4 . Ei au citit: doisprezece este la trei, precum șaisprezece este la patru. Aici 12 și 4 sunt membrii extremi ai proporției, iar 3 și 16 sunt membrii de mijloc ai proporției.
Proprietatea de bază a proporției.
Produsul termenilor extremi ai unei proporții este egal cu produsul termenilor ei medii.
Pentru proporție a :b =c :d sau a/b=c/d proprietatea principală este scrisă astfel: a d \u003d b c .
Pentru proporția noastră 12 : 3 = 16 : 4 proprietatea principală se va scrie astfel: 12 4 = 3 16 . Se pare că este egalitatea corectă: 48 \u003d 48 .
Pentru a găsi termenul extrem necunoscut al proporției, trebuie să împărțiți produsul termenilor medii ai proporției la termenul extrem cunoscut.
Exemple.
1) x: 20 = 2: 5. Avem XȘi 5 sunt membrii extremi ai proporției și 20 Și 2 - mediu.
Soluţie.
x = (20 2):5- trebuie să înmulțiți termenii de mijloc ( 20 Și 2 ) și împărțiți rezultatul la termenul extrem cunoscut (număr 5 );
x=40:5 este produsul termenilor de mijloc ( 40 ) împărțiți la termenul extrem cunoscut ( 5 );
x = 8. Am obținut termenul extrem dorit al proporției.
Este mai convenabil să scrieți constatarea unui membru necunoscut al proporției folosind o fracție obișnuită. Iată cum ar fi scris atunci exemplul pe care l-am luat în considerare:
Termenul extrem dorit al proporției ( X) va fi egal cu produsul termenilor de mijloc ( 20 Și 2 ) împărțit la termenul extrem cunoscut ( 5 ).
Reducem fracția cu 5 (împarte la 5 X.
Mai multe astfel de exemple de găsire a unui membru extrem necunoscut al proporției.

Pentru a găsi termenul mediu necunoscut al proporției, trebuie să împărțiți produsul termenilor extremi ai proporției la termenul mediu cunoscut.
Exemple. Găsiți termenul mediu necunoscut al proporției.
5) 9: x = 3: 14. Număr 3 este termenul mediu cunoscut al proporției date, numere 9 Și 14 sunt termenii extremi ai proporției.
Soluţie.
x \u003d (9 14): 3 -înmulțiți termenii extremi ai proporției și împărțiți rezultatul la termenul mediu cunoscut al proporției;
x= 136:3;
x=42.
Soluția acestui exemplu poate fi scrisă diferit:
 Termenul mediu necesar al proporției ( X) va fi egal cu produsul termenilor extremi ( 9
Și 14
) împărțit la termenul mediu cunoscut ( 3
).
Termenul mediu necesar al proporției ( X) va fi egal cu produsul termenilor extremi ( 9
Și 14
) împărțit la termenul mediu cunoscut ( 3
).
Reducem fracția cu 3 (împarte la 3 iar numărătorul și numitorul unei fracții). Găsirea valorii X.
Dacă ați uitat cum să reduceți fracțiile obișnuite, repetați subiectul: ""
Mai multe astfel de exemple despre găsirea membrului mediu necunoscut al proporției.

Secțiuni: Matematică
Tip de lecție: Lecție de studiu și consolidare primară a noilor cunoștințe.
Forma lecție: Lecție-cercetare.
Obiectivele lecției:
- să activeze activitatea cognitivă a elevilor;
- introducerea elevilor în conceptele: proporție, membrii proporției; proporții corecte și incorecte;
- de a introduce elevii în proprietatea de bază a proporției și de a-și forma deprinderea de a determina proporția corectă.
Echipament:
Fișele de traseu indică punctele care pot fi obținute pentru rezolvarea sarcinilor. La punctare, elevul ține cont de corectitudinea deciziei sale, de rapiditatea deciziei (autoverificare și verificare reciprocă cu ajutorul prezentării). În rândul „Puncte suplimentare”, se acordă puncte pentru răspunsul la întrebări suplimentare, pentru a ajuta profesorul să organizeze testarea altor elevi și, de asemenea, pentru „ghicirea” temei lecției.
Cardurile sunt tăiate și distribuite în plicuri studenților (un plic pe birou).
3. Carduri pentru o placă magnetică (Figura 1, Figura 2, Figura 3)
În timpul lecției, aceste carduri sunt postate pe o tablă magnetică.
4. Puzzle-uri (Figura 4, Figura 5, Figura 6, Figura 7).




Rebusurile compilate de elevii de liceu (cu excepția rebusului „Proporție” - acest rebus a fost luat dintr-o lecție prezentată la FPI de profesorul Kozak Tatyana Ivanovna, școala gimnazială nr. 20 Progress, Regiunea Amur) se află pe tablă, elevii sunt invitat să le rezolve după lecție.
Echipamentul tehnic al lecției este un computer, un proiector pentru demonstrarea unei prezentări, un ecran. Prezentare pe computer în Microsoft PowerPoint (Anexa 4).
I. Organizarea începutului lecției
Buna ziua! Vă rugăm să verificați dacă aveți fișe pe birou, dacă aveți un creion roșu și albastru și că sunteți pregătit pentru lecție.
II. Subiectele mesajului, scopurile și obiectivele lecției.
Astăzi la lecție continuăm să studiem o secțiune mare a cursului de matematică. Am terminat de studiat subiectul (ce? - "Atitudine"). Acum începem să explorăm un subiect nou în această secțiune. Câteva exemple ne vor ajuta să înțelegem subiectul lecției. Pe pagina de titlu a foii de traseu, trebuie să completați tabelul rezolvând exemplele oral și apoi veți cunoaște subiectul lecției de astăzi. Slide 1
Deci, subiectul lecției de astăzi Proporţie. Slide 2
Cunoscând subiectul lecției, încercați să faceți un plan de lecție. Ce ar trebui să înveți în clasă astăzi? Ce vrei sa stii? Ce vrei să înveți la clasă?
Vom face un plan, pe care îl vom completa în timpul lecției. (elevii numesc primele două și ultimele două puncte ale planului, restul se completează în timpul lecției, pe măsură ce se „descoperă” noi cunoștințe; planul lecției este scris pe tablă)
- repetiție (întrebări legate de atitudine)
Definiţia proportion
MEMBRII PROPORȚIEI
PROPORȚII DREPTATE ȘI INCORECTE
PRINCIPALE PROPRIETĂȚI ALE PROPORȚIEI
Aplicație în matematică
Aplicație în viață
Ultimele două puncte le vom putea analiza în lecțiile următoare, pe măsură ce studiem tema.
III. Actualizarea cunoștințelor elevilor. Pregătirea pentru activitatea educațională și cognitivă activă în etapa principală a lecției.
Discutați întrebări legate de subiectul „Atitudine” cu un coleg de clasă.
Cine este gata să pună întrebări legate de ultimul subiect? (viscol) MP1
- Ce este o atitudine?
Cum poți scrie o relație?
La ce întrebări răspunde atitudinea?
Cum poți scrie raportul a două numere?
Ce poate înlocui semnul Do?
De ce crezi că am repetat aceste concepte?
Ne vor ajuta atunci când învățăm un subiect nou.
Ia plicurile și alcătuiește relația A La bȘi c La d doua feluri. (doar 4 relații) MUNCĂ ÎN PERECHI.
MP2 Ai mai multe relații în fața ta. Găsiți semnificația acestor expresii. Slide 3
4: 0,5= = 5: 10 = = 8: 1 = 2,5: 5 =
Grupați relațiile după un anumit atribut și faceți egalitățile corespunzătoare.
IV. Asimilarea noilor cunoștințe.
4: 0,5 = 8: 1 = 5: 10 = 2,5: 5
Pe ce bază ați grupat aceste relații?
- Valorile lor sunt egale.
Egalitățile rezultate se numesc proporții.
Gândește și definește proporția.
SUGESTIE - proporția este... PE ECRAN ( egalitate)
Egalitatea de... CE ( relaţii)
Câte relații? ( Două).
Cine este sigur de părerea lui, notează definiția în foaia de traseu. MP3
Cine este gata să meargă la tablă și să elaboreze o definiție a proporției? (Anexa 3)
DEFINIȚIE (pe o tablă magnetică): Proporția este egalitatea a două rapoarte.
Să ne uităm la interpretarea cuvântului proporție în dicționarul limbii ruse Ozhegov S.I. Slide 4: „Proporția este un anumit raport de părți între ele, proporționalitate. În matematică, egalitatea a două rapoarte.Ați formulat definiția proporției, precum și în dicționarul limbii ruse!
Gândiți-vă la ce termen matematic este în consonanță cuvântul „proporție”? ( interes). Cum se traduce termenul „procent”? ( de la o sută). Deci, „pro” este tradus ca „de la”. Ce parte din cuvânt a mai rămas? (“ o porțiune”). Unde ai dat peste acest cuvânt? (la gatit) Ce înseamnă? ( mărimea)
Cuvântul proporție provine din cuvântul latin proportio - proporționalitate. (dicționar etimologic). Slide 4
Folosind definiția proporției, scrieți proporții folosind semnul diviziunii și bara fracțională. (LUCRĂ ÎN PERECHI, plicuri).
În foile de traseu, notați proporția folosind literele a, b, c, d. MP4
Și acum vom afla cum se numesc numerele care alcătuiesc proporția.
Numerele a, b, c, d numiti membri ai proportiei
Care este primul și ultimul termen al proporției? ( a și c)
Și cum se numește de obicei (în viață) primul și ultimul? (extrem)
Deci termenii a și b se numesc ...? (extrem)
Unde sunt termenii c și d? (În mijloc)
Și care sunt numele membrilor c și d? ( mediu)
Ce membri sunt evidențiați cu roșu? ( La din timp)
culoare (Cu rar) membrii.membrii mijlocii

Să revenim la planul de lecție - ai ceva de adăugat la el? (membrii extremi și medii ai proporției)
V. Consolidarea primară a cunoştinţelor
MP5 Completați tabelul:
Ce concluzie se poate trage? Înregistrați rezultatul pe itinerar. ( Proporțional, produsul termenilor extremi este egal cu produsul termenilor de mijloc)Slide 8
MP6 Iată cinci egalități. Sunt toate proporții?
Subliniază proporțiile.
= ; 7 + 11 = 36: 2; 72: 9 = 16: 2; = 20: 4; 5 40 = 100 2SLIDE 7 Ridică-te, cine a terminat.
Toată lumea este sigură că aici sunt trei proporții? Într-adevăr, în ultima egalitate, produsul termenilor extremi nu este egal cu produsul celor mijlocii. Să revenim la definiția proporției ( Proporție - egalitatea a două rapoarte). Este a treia egalitate egalitatea celor două relații? (este). Prin definiție, este o proporție? (Da). Este produsul termenilor extremi egal cu produsul termenilor medii? (Nu). Deci este o proporție...? (gresit). Această proporție se numește incorectă. Deci, există proporții incorecte și...? (credincios). Formulați proprietatea principală a proporției, folosind cunoștințele acumulate. (În proporția corectă, produsul termenilor extremi este egal cu produsul celor din mijloc).
VI. Consolidarea cunoștințelor.
Completați tabelul.
Proporție corectă Proporție greșită
= = 20: 4
Cum altfel poți determina proporția corectă sau cea greșită? (aflați valoarea relației)
În viitor, vom vorbi despre proporțiile corecte.
Să revenim la planul de lecție. Ce se poate adauga? (proporții corecte și incorecte)
MP7 Folosind literele B și H, marcați proporțiile corecte și incorecte.
= 1: 0,5 = 4,8: 2,4 7,5: 5 = 2: 3 = 10: 3 = 3 : 1 5:x = 20:4x
VII. Generalizare și sistematizare.
MP8 Folosind proprietatea de bază a proporției, alcătuiți proporția corectă din următoarele numere: 4, 5, 12, 15. Câte proporții corecte puteți face?
VIII. Controlul și autotestarea cunoștințelor
MP9 Dictare matematică
- Scrieți proporția: numărul 18 este legat de 4, deoarece 27 este legat de 6.
- Scrieți proporția: raportul de la trei la cinci este egal cu raportul de la doi la șapte.
- Notați termenii medii ai proporției: 1,5: 2 \u003d 4,5: 6
- Notați membrii extremi ai proporției: 2/1,9 = 3/2,8
- Este corectă proporția de la punctul 3?
- Este corectă proporția de la punctul 4?
- Este adevărată afirmația: rădăcina ecuației este 20/5 \u003d x / 0,5 numărul 2
- Este adevărată următoarea afirmație: Orice patru numere naturale pot fi folosite pentru a forma o proporție?
DIAPOSITIVA 10. Evaluare inter pares
IX. Rezumând lecția.
Vă rugăm să consultați planul de lecție.
Ce ai învățat astăzi în clasă? (ce este o proporție, în ce constă o proporție, proporțiile sunt adevărate și incorecte, proprietatea principală a unei proporții, ...)
Ce ai învățat astăzi în clasă? (determinați membrii extremi și medii ai proporției, aflați dacă proporția este corectă sau incorectă, ...)
Ce alte întrebări pot fi puse la sfârșitul lecției?
-Câte proporții corecte se pot face din această proporție corectă?
Cum poți spune dacă o proporție este corectă sau greșită?
Să ne amintim ultima sarcină a dictatului matematic.
Orice patru numere naturale pot fi folosite pentru a forma o proporție. Răspunsul corect este DA. Puteți întocmi o proporție, dar nu va fi neapărat corectă.
Din fraza " Orice patru numere naturale pot fi folosite pentru a forma o proporție. Eliminați un cuvânt pentru a face această afirmație incorectă. (natural). De ce? (Numărul 0 nu poate fi membru al unei proporții). Orice patru numere pot fi folosite pentru a forma o proporție
În această frază Orice patru numere naturale pot fi folosite pentru a forma o proporție. introduceți un cuvânt pentru a face afirmația incorectă (Adevărat). Din oricare patru numere naturale, puteți face proporția corectă.
Calculați numărul de puncte pe care le-ați câștigat la lecție și acordați o notă.
X. Informații despre teme și instrucțiuni despre cum să le completezi
Matematică - 6, Vilenkin N.Ya. et al., ediţia a 6-a
P.21, nr. 760, 781, 782, 783 (a)
Raportul a două numere
Definiția 1
Raportul a două numere este privatul lor.
Exemplul 1
raportul de $18$ la $3$ poate fi scris astfel:
$18\div 3=\frac(18)(3)=6$.
raportul de $5$ la $15$ poate fi scris astfel:
$5\div 15=\frac(5)(15)=\frac(1)(3)$.
Prin utilizarea raportul a două numere poate fi afișat:
- de câte ori un număr este mai mare decât altul;
- ce parte reprezintă un număr din altul.
Când se întocmește raportul a două numere în numitorul unei fracții, notează numărul cu care se face comparația.
Cel mai adesea, un astfel de număr urmează cuvintele „comparativ cu...” sau prepoziției „la...”.
Amintiți-vă proprietatea de bază a unei fracții și aplicați-o unei relații:
Observația 1
Când înmulțim sau împărțim ambii termeni ai relației cu același număr, altul decât zero, obținem un raport care este egal cu cel inițial.
Luați în considerare un exemplu care ilustrează utilizarea conceptului de raport de două numere.
Exemplul 2
Cantitatea de precipitații în luna anterioară a fost de $195$ mm, iar în luna curentă - $780$ mm. Cu cât a crescut cantitatea de precipitații din luna curentă față de luna anterioară?
Soluţie.
Compuneți raportul dintre cantitatea de precipitații din luna curentă și cantitatea de precipitații din luna anterioară:
$\frac(780)(195)=\frac(780\div 5)(195\div 5)=\frac(156\div 3)(39\div 3)=\frac(52)(13)=4 $.
Răspuns: cantitatea de precipitații în luna curentă este de $4$ ori mai mare decât în luna anterioară.
Exemplul 3
Aflați de câte ori numărul $1 \frac(1)(2)$ este conținut în numărul $13 \frac(1)(2)$.
Soluţie.
$13 \frac(1)(2)\div 1 \frac(1)(2)=\frac(27)(2)\div \frac(3)(2)=\frac(27)(2) \cdot \frac(2)(3)=\frac(27)(3)=9$.
Răspuns: $9$ ori.
Conceptul de proporție
Definiția 2
Proporţie se numește egalitatea a două relații:
$a\div b=c\div d$
$\frac(a)(b)=\frac(c)(d)$.
Exemplul 4
$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,
$\frac(8)(2)=\frac(36)(9)$, $\frac(10)(40)=\frac(9)(36)$, $\frac(15)(75)= \frac(1)(5)$.
În proporția $\frac(a)(b)=\frac(c)(d)$ (sau $a:b = c\div d$), numerele a și d se numesc membrii extremi proporții, în timp ce numerele $b$ și $c$ sunt membrii mijlocii proporții.
Proporția corectă poate fi convertită după cum urmează:
Observația 2
Produsul termenilor extremi ai proporției corecte este egal cu produsul termenilor de mijloc:
$a \cdot d=b \cdot c$.
Această afirmație este proprietatea de bază a proporției.
Este adevărat și invers:
Observația 3
Dacă produsul termenilor extremi ai unei proporții este egal cu produsul termenilor ei medii, atunci proporția este corectă.
Observația 4
Dacă termenii de mijloc sau termenii extremi sunt rearanjați în proporția corectă, atunci proporțiile care vor fi obținute vor fi și ele corecte.
Exemplul 5
$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,
$\frac(2)(8)=\frac(9)(36)$, $\frac(40)(10)=\frac(36)(9)$, $\frac(75)(15)= \frac(5)(1)$.
Folosind această proprietate, este ușor să găsiți un termen necunoscut dintr-o proporție dacă ceilalți trei sunt cunoscuți:
$a=\frac(b \cdot c)(d)$; $b=\frac(a \cdot d)(c)$; $c=\frac(a \cdot d)(b)$; $d=\frac(b \cdot c)(a)$.
Exemplul 6
$\frac(6)(a)=\frac(16)(8)$;
$6 \cdot 8=16 \cdot a$;
$16 \cdot a=6 \cdot 8$;
$16 \cdot a=48$;
$a=\frac(48)(16)$;
Exemplul 7
$\frac(a)(21)=\frac(8)(24)$;
$a \cdot 24=21 \cdot 8$;
$a \cdot 24=168$;
$a=\frac(168)(24)$;
3 dolari grădinar - 108 dolari copaci;
$x$ grădinari - $252$ copac.
Să facem o proporție:
$\frac(3)(x)=\frac(108)(252)$.
Să folosim regula pentru găsirea termenului necunoscut al proporției:
$b=\frac(a \cdot d)(c)$;
$x=\frac(3 \cdot 252)(108)$;
$x=\frac(252)(36)$;
Răspuns: Grădinarii vor avea nevoie de 7$ pentru a tăia copacii de 252$.
Cel mai adesea, proprietățile proporției sunt utilizate în practică în calculele matematice în cazurile în care este necesar să se calculeze valoarea unui membru necunoscut al proporției, dacă sunt cunoscute valorile celorlalți trei membri.
