Ako urobiť správny pomer. Ako vypočítať pomer. Ako vyriešiť problém pomocou pomeru

Jednoducho povedané, ide o zeleninu varenú vo vode podľa špeciálnej receptúry. Zvážim dve počiatočné zložky (zeleninový šalát a vodu) a konečný výsledok - boršč. Geometricky to môže byť znázornené ako obdĺžnik, v ktorom jedna strana označuje šalát a druhá strana vodu. Súčet týchto dvoch strán bude označovať boršč. Uhlopriečka a plocha takéhoto obdĺžnika „boršč“ sú čisto matematické pojmy a nikdy sa nepoužívajú v receptoch na boršč.

Ako sa z matematického hľadiska zmení šalát a voda na boršč? Ako sa môže súčet dvoch segmentov zmeniť na trigonometriu? Aby sme to pochopili, potrebujeme funkcie lineárnych uhlov.

V učebniciach matematiky nenájdete nič o lineárnych uhlových funkciách. Ale bez nich nemôže existovať matematika. Zákony matematiky, rovnako ako zákony prírody, fungujú, či už vieme, že existujú alebo nie.

Lineárne uhlové funkcie sú zákony sčítania. Pozrite sa, ako sa algebra mení na geometriu a geometria na trigonometriu.

Je možné sa zaobísť bez lineárnych uhlových funkcií? Môžete, pretože matematici sa zaobídu aj bez nich. Trik matematikov spočíva v tom, že nám vždy hovoria len o tých problémoch, ktoré sami vedia vyriešiť, a nikdy nám nehovoria o problémoch, ktoré nevedia vyriešiť. Pozri. Ak poznáme výsledok sčítania a jedného člena, pomocou odčítania nájdeme druhý člen. Všetky. Iné problémy nepoznáme a nie sme schopní ich riešiť. Čo robiť, ak poznáme len výsledok sčítania a nepoznáme oba pojmy? V tomto prípade je potrebné výsledok sčítania rozložiť na dva členy pomocou lineárnych uhlových funkcií. Ďalej si sami vyberáme, čo môže byť jeden člen, a lineárne uhlové funkcie ukazujú, aký by mal byť druhý člen, aby bol výsledok sčítania presne taký, aký potrebujeme. Takýchto dvojíc výrazov môže byť nekonečné množstvo. V bežnom živote nám to ide veľmi dobre bez rozkladu súčtu, stačí nám odčítanie. Ale pri vedeckých štúdiách prírodných zákonov môže byť rozšírenie sumy na pojmy veľmi užitočné.

Ďalší zákon sčítania, o ktorom matematici neradi hovoria (ďalší ich trik), vyžaduje, aby výrazy mali rovnakú mernú jednotku. Pre šalát, vodu a boršč to môžu byť jednotky hmotnosti, objemu, ceny alebo mernej jednotky.

Obrázok ukazuje dve úrovne rozdielu pre matematiku. Prvou úrovňou sú rozdiely v poli čísel, ktoré sú uvedené a, b, c. Toto robia matematici. Druhou úrovňou sú rozdiely v oblasti meracích jednotiek, ktoré sú uvedené v hranatých zátvorkách a sú označené písmenom U. Toto robia fyzici. Môžeme chápať tretiu rovinu – rozdiely v rozsahu popisovaných objektov. Rôzne objekty môžu mať rovnaký počet rovnakých merných jednotiek. Aké dôležité to je, môžeme vidieť na príklade borščovej trigonometrie. Ak k rovnakému zápisu pre merné jednotky rôznych objektov pridáme dolné indexy, môžeme presne povedať, aká matematická veličina opisuje konkrétny objekt a ako sa mení v čase alebo v súvislosti s našimi činmi. list W Vodu označím písmenom SŠalát označím písmenom B- boršč. Tu je návod, ako by vyzerali funkcie lineárneho uhla pre boršč.

Ak zoberieme časť vody a časť šalátu, razom sa premenia na jednu porciu boršču. Tu vám navrhujem, aby ste si trochu oddýchli od boršču a zaspomínali si na svoje vzdialené detstvo. Pamätáte si, ako nás učili spájať zajačiky a kačice? Bolo potrebné zistiť, koľko zvierat sa ukáže. Čo nás potom naučili robiť? Naučili nás oddeľovať jednotky od čísel a sčítať čísla. Áno, k akémukoľvek inému číslu je možné pridať akékoľvek číslo. Toto je priama cesta k autizmu modernej matematiky – nerozumieme čomu, nie je jasné prečo a veľmi zle chápeme, ako to súvisí s realitou, pretože matematici fungujú len na jednej úrovni. Bude správnejšie naučiť sa prechádzať z jednej meracej jednotky do druhej.

A zajačiky, kačice a malé zvieratká sa dajú spočítať na kusy. Jedna spoločná jednotka merania pre rôzne objekty nám umožňuje ich sčítanie. Toto je detská verzia problému. Pozrime sa na podobný problém pre dospelých. Čo získate, keď pridáte zajačikov a peniaze? Tu sú dve možné riešenia.

Prvá možnosť. Určíme trhovú hodnotu zajačikov a pripočítame ju k dostupnej hotovosti. Dostali sme celkovú hodnotu nášho bohatstva v peniazoch.

Druhá možnosť. K počtu bankoviek, ktoré máme, môžete pridať počet zajačikov. Množstvo hnuteľného majetku dostaneme na kusy.

Ako vidíte, rovnaký zákon sčítania vám umožňuje získať rôzne výsledky. Všetko závisí od toho, čo presne chceme vedieť.

Ale späť k nášmu boršču. Teraz môžeme vidieť, čo sa stane pre rôzne hodnoty uhla funkcií lineárneho uhla.

Uhol je nulový. Máme šalát, ale bez vody. Nemôžeme variť boršč. Množstvo boršču je tiež nulové. To vôbec neznamená, že nulový boršč sa rovná nule vody. Nulový boršč môže byť aj pri nulovom šaláte (pravom uhle).

Pre mňa osobne je to hlavný matematický dôkaz toho, že . Nula po pridaní číslo nezmení. Je to preto, že samotné sčítanie je nemožné, ak existuje iba jeden výraz a druhý výraz chýba. Môžete sa k tomu vzťahovať ako chcete, ale pamätajte – všetky matematické operácie s nulou vymysleli samotní matematici, takže zahoďte logiku a hlúpo napchajte definície vymyslené matematikmi: „delenie nulou je nemožné“, „akékoľvek číslo vynásobené nulou“ rovná sa nule“ , „za bodom nula“ a iné nezmysly. Stačí si raz zapamätať, že nula nie je číslo, a už nikdy nebudete mať otázku, či je nula prirodzené číslo alebo nie, pretože takáto otázka vo všeobecnosti stráca zmysel: ako možno považovať číslo za číslo, ktoré nie je číslo? . Je to ako pýtať sa, akej farbe pripísať neviditeľnú farbu. Pridanie nuly k číslu je ako maľovanie farbou, ktorá neexistuje. Zamávali suchým štetcom a všetkým povedali, že „máme natreté“. Ale to som trochu odbočil.

Uhol je väčší ako nula, ale menší ako štyridsaťpäť stupňov. Máme veľa šalátu, ale málo vody. V dôsledku toho získame hustý boršč.

Uhol je štyridsaťpäť stupňov. Máme rovnaké množstvo vody a šalátu. Toto je perfektný boršč (nech mi kuchárky odpustia, je to len matematika).

Uhol je väčší ako štyridsaťpäť stupňov, ale menší ako deväťdesiat stupňov. Máme veľa vody a málo šalátu. Získajte tekutý boršč.

Pravý uhol. Máme vodu. Na šalát ostali len spomienky, keďže pokračujeme v meraní uhla od čiary, ktorá kedysi šalát označovala. Nemôžeme variť boršč. Množstvo boršču je nulové. V takom prípade vydržte a pite vodu, kým je k dispozícii)))

Tu. Niečo také. Môžem tu rozprávať ďalšie príbehy, ktoré tu budú viac než vhodné.

Dvaja priatelia mali svoje podiely v spoločnom obchode. Po vražde jedného z nich prešlo všetko k druhému.

Vznik matematiky na našej planéte.

Všetky tieto príbehy sú rozprávané jazykom matematiky pomocou lineárnych uhlových funkcií. Inokedy vám ukážem skutočné miesto týchto funkcií v štruktúre matematiky. Medzitým sa vráťme k trigonometrii boršču a zvážme projekcie.

Sobota 26. októbra 2019

Streda 7. augusta 2019

Na záver rozhovoru o , musíme zvážiť nekonečnú množinu. Z toho vyplýva, že pojem „nekonečno“ pôsobí na matematikov ako boa constrictor na králika. Chvejúca sa hrôza z nekonečna pripravuje matematikov o zdravý rozum. Tu je príklad:

Pôvodný zdroj sa nachádza. Alfa označuje reálne číslo. Znamienko rovnosti vo vyššie uvedených výrazoch znamená, že ak k nekonečnu pridáte číslo alebo nekonečno, nič sa nezmení, výsledkom bude rovnaké nekonečno. Ak vezmeme ako príklad nekonečnú množinu prirodzených čísel, uvažované príklady možno znázorniť takto:

Aby matematici vizuálne dokázali svoj prípad, prišli s mnohými rôznymi metódami. Osobne sa na všetky tieto metódy pozerám ako na tance šamanov s tamburínami. V podstate všetci prídu na to, že buď nie sú niektoré izby obsadené a usadia sa v nich noví hostia, alebo časť návštevníkov vyhodí na chodbu, aby uvoľnili miesto pre hostí (veľmi ľudsky). Svoj pohľad na takéto rozhodnutia som prezentovala formou fantastického príbehu o Blondínke. Na čom je založená moja úvaha? Presun nekonečného počtu návštevníkov trvá nekonečne dlho. Po tom, ako uvoľníme prvú hosťovskú izbu, bude vždy jeden z návštevníkov chodiť po chodbe zo svojej izby do ďalšej až do konca času. Časový faktor sa samozrejme dá hlúpo ignorovať, ale toto už bude z kategórie „zákon nie je písaný pre hlupákov“. Všetko závisí od toho, čo robíme: prispôsobujeme realitu matematickým teóriám alebo naopak.

Čo je to „nekonečný hotel“? Infinity inn je hostinec, ktorý má vždy ľubovoľný počet voľných miest, bez ohľadu na to, koľko izieb je obsadených. Ak sú všetky izby v nekonečnej chodbe „pre návštevy“ obsadené, je tu ďalšia nekonečná chodba s izbami pre „hostí“. Takýchto chodieb bude nekonečne veľa. Zároveň má „nekonečný hotel“ nekonečný počet poschodí v nekonečnom množstve budov na nekonečnom počte planét v nekonečnom množstve vesmírov vytvorených nekonečným počtom Bohov. Na druhej strane matematici sa nedokážu vzdialiť od banálnych každodenných problémov: Boh-Alah-Budha je vždy len jeden, hotel je jeden, chodba je len jedna. Matematici sa teda pokúšajú žonglovať s poradovými číslami hotelových izieb a presviedčajú nás, že je možné „strčiť do nešťastia“.

Logiku môjho uvažovania vám predvediem na príklade nekonečnej množiny prirodzených čísel. Najprv musíte odpovedať na veľmi jednoduchú otázku: koľko množín prirodzených čísel existuje - jedna alebo veľa? Na túto otázku neexistuje správna odpoveď, keďže sme sami vymysleli čísla, v prírode žiadne čísla nie sú. Áno, príroda vie perfektne počítať, ale na to používa iné matematické nástroje, ktoré nám nie sú známe. Ako si príroda myslí, to vám poviem inokedy. Keďže sme vymysleli čísla, sami rozhodneme, koľko množín prirodzených čísel existuje. Zvážte obe možnosti, ako sa na skutočného vedca patrí.

Možnosť jedna. „Dajme nám“ jednu množinu prirodzených čísel, ktorá pokojne leží na poličke. Berieme túto sadu z police. To je všetko, na poličke nezostali žiadne ďalšie prirodzené čísla a nie je ich ani kde vziať. Do tejto sady nemôžeme pridať jeden, pretože ho už máme. Čo ak naozaj chcete? Žiaden problém. Môžeme zobrať jednotku z už odobratej sady a vrátiť ju do police. Potom môžeme z police vybrať jednotku a pridať ju k tomu, čo nám zostalo. Výsledkom je, že opäť dostaneme nekonečnú množinu prirodzených čísel. Všetky naše manipulácie môžete napísať takto:

Zapísal som operácie v algebraickom zápise a zápise teórie množín s podrobným zoznamom prvkov množiny. Dolný index naznačuje, že máme jednu a jedinú množinu prirodzených čísel. Ukazuje sa, že množina prirodzených čísel zostane nezmenená iba vtedy, ak sa od nej jedno odčíta a rovnaké sa pridá.

Možnosť dva. Na poličke máme veľa rôznych nekonečných množín prirodzených čísel. Zdôrazňujem – INÉ, napriek tomu, že sú prakticky na nerozoznanie. Berieme jednu z týchto sád. Potom vezmeme jedno z inej množiny prirodzených čísel a pridáme ho k množine, ktorú sme už zobrali. Môžeme dokonca sčítať dve sady prirodzených čísel. Tu je to, čo dostaneme:

Dolné indexy „jeden“ a „dva“ označujú, že tieto prvky patrili do rôznych súborov. Áno, ak pridáte jednu do nekonečnej množiny, výsledkom bude tiež nekonečná množina, ale nebude rovnaká ako pôvodná množina. Ak sa k jednej nekonečnej množine pridá ďalšia nekonečná množina, výsledkom je nová nekonečná množina pozostávajúca z prvkov prvých dvoch množín.

Množina prirodzených čísel sa používa na počítanie rovnako ako pravítko na meranie. Teraz si predstavte, že ste pridali jeden centimeter na pravítko. Toto už bude iný riadok, ktorý sa nebude rovnať pôvodnému.

Môžete prijať alebo neprijať moje odôvodnenie - je to vaša vec. Ale ak niekedy narazíte na matematické problémy, zvážte, či nie ste na ceste falošného uvažovania, šliapaného generáciami matematikov. Hodiny matematiky v nás totiž v prvom rade vytvárajú ustálený stereotyp myslenia a až potom nám pridávajú rozumové schopnosti (alebo naopak oberajú o slobodné myslenie).

pozg.ru

Nedeľa 4. augusta 2019

Písal som dodatok k článku o a videl som tento úžasný text na Wikipédii:

Čítame: „...bohatý teoretický základ babylonskej matematiky nemal holistický charakter a bol zredukovaný na súbor rôznorodých techník, bez spoločného systému a dôkazovej základne.“

Wow! Akí sme šikovní a ako dobre vieme vidieť nedostatky druhých. Je pre nás slabé pozerať sa na modernú matematiku v rovnakom kontexte? Mierne parafrázujúc vyššie uvedený text, osobne som dostal nasledovné:

Bohatý teoretický základ modernej matematiky nemá holistický charakter a je redukovaný na súbor nesúrodých sekcií, bez spoločného systému a dôkazovej základne.

Nebudem chodiť ďaleko, aby som potvrdil svoje slová – má jazyk a konvencie, ktoré sú odlišné od jazyka a konvencií mnohých iných odvetví matematiky. Rovnaké názvy v rôznych odvetviach matematiky môžu mať rôzny význam. Najzrejmejším omylom modernej matematiky chcem venovať celý cyklus publikácií. Do skorého videnia.

Sobota 3. augusta 2019

Ako rozdeliť množinu na podmnožiny? Ak to chcete urobiť, musíte zadať novú mernú jednotku, ktorá sa nachádza v niektorých prvkoch vybranej sady. Zvážte príklad.

Nech máme veľa A pozostávajúci zo štyroch ľudí. Tento súbor je tvorený na základe "ľudí" Označme prvky tohto súboru prostredníctvom písmena A, dolný index s číslom bude označovať poradové číslo každej osoby v tomto súbore. Predstavme si novú mernú jednotku „sexuálna charakteristika“ a označme ju písmenom b. Keďže sexuálne vlastnosti sú vlastné všetkým ľuďom, znásobujeme každý prvok súboru A o pohlaví b. Všimnite si, že naša množina „ľudia“ sa teraz stala množinou „ľudia s pohlavím“. Potom môžeme rozdeliť pohlavné znaky na mužské bm a dámske bw rodové charakteristiky. Teraz môžeme použiť matematický filter: vyberieme jednu z týchto sexuálnych charakteristík, nezáleží na tom, ktorá je mužská alebo ženská. Ak je v človeku prítomný, tak ho vynásobíme jednou, ak taký znak neexistuje, vynásobíme ho nulou. A potom aplikujeme obvyklú školskú matematiku. Pozrite sa, čo sa stalo.

Po vynásobení, redukciách a preskupeniach sme dostali dve podmnožiny: mužskú podmnožinu bm a podskupina žien bw. Približne rovnakým spôsobom uvažujú matematici, keď aplikujú teóriu množín v praxi. Ale nepúšťajú nás do detailov, ale dávajú nám konečný výsledok – „veľa ľudí pozostáva z podskupiny mužov a podskupiny žien“. Prirodzene, môžete mať otázku, ako správne aplikovať matematiku vo vyššie uvedených transformáciách? Dovolím si vás ubezpečiť, že v skutočnosti sú transformácie urobené správne, stačí poznať matematické opodstatnenie aritmetiky, Booleovej algebry a iných úsekov matematiky. Čo to je? Inokedy vám o tom poviem.

Čo sa týka nadmnožín, je možné spojiť dve sady do jednej nadmnožiny výberom mernej jednotky, ktorá je prítomná v prvkoch týchto dvoch sád.

Ako vidíte, jednotky merania a bežná matematika robia z teórie množín minulosť. Znakom toho, že s teóriou množín nie je všetko v poriadku, je to, že matematici prišli s vlastným jazykom a notáciou pre teóriu množín. Matematici robili to, čo kedysi robili šamani. Len šamani vedia „správne“ uplatniť svoje „vedomosti“. Tieto „vedomosti“ nás učia.

Nakoniec vám chcem ukázať, ako matematici manipulujú .

Pondelok 7. januára 2019

V piatom storočí pred Kristom sformuloval staroveký grécky filozof Zenón z Elea svoje slávne apórie, z ktorých najznámejšia je apória „Achilles a korytnačka“. Znie to takto:

Povedzme, že Achilles beží desaťkrát rýchlejšie ako korytnačka a je za ňou tisíc krokov. Počas doby, počas ktorej Achilles prebehne túto vzdialenosť, sa korytnačka plazí sto krokov rovnakým smerom. Keď Achilles prebehne sto krokov, korytnačka sa plazí ďalších desať krokov atď. Proces bude pokračovať donekonečna, Achilles korytnačku nikdy nedohoní.

Táto úvaha sa stala logickým šokom pre všetky nasledujúce generácie. Aristoteles, Diogenes, Kant, Hegel, Gilbert... Všetci tak či onak považovali Zenónove apórie. Šok bol taký silný, že " ... diskusie pokračujú aj v súčasnosti, vo vedeckej komunite sa zatiaľ nepodarilo dospieť k jednotnému názoru na podstatu paradoxov ... do skúmania problematiky bola zapojená matematická analýza, teória množín, nové fyzikálne a filozofické prístupy ; žiadna z nich sa nestala všeobecne akceptovaným riešením problému ..."[Wikipedia," Zeno's Aporias "]. Každý chápe, že je oklamaný, ale nikto nechápe, čo je to podvod.

Z pohľadu matematiky Zenón vo svojich apóriách jasne demonštroval prechod od hodnoty k. Tento prechod znamená použitie namiesto konštánt. Pokiaľ som pochopil, matematický aparát na aplikáciu premenných jednotiek merania buď ešte nebol vyvinutý, alebo nebol aplikovaný na Zenónove apórie. Aplikácia našej bežnej logiky nás vedie do pasce. My zotrvačnosťou myslenia aplikujeme konštantné jednotky času na recipročné. Z fyzického hľadiska to vyzerá tak, že sa čas spomalí až úplne zastaví v momente, keď Achilles dobehne korytnačku. Ak sa čas zastaví, Achilles už nemôže predbehnúť korytnačku.

Ak otočíme logiku, na ktorú sme zvyknutí, všetko zapadne na svoje miesto. Achilles beží konštantnou rýchlosťou. Každý nasledujúci segment jeho cesty je desaťkrát kratší ako predchádzajúci. Čas strávený na jeho prekonanie je teda desaťkrát kratší ako ten predchádzajúci. Ak v tejto situácii použijeme pojem „nekonečno“, potom by bolo správne povedať „Achilles nekonečne rýchlo predbehne korytnačku“.

Ako sa vyhnúť tejto logickej pasci? Zostaňte v konštantných jednotkách času a neprechádzajte na recipročné hodnoty. V Zenónovom jazyku to vyzerá takto:

Za čas, ktorý Achilles potrebuje prejsť tisíc krokov, sa korytnačka plazí sto krokov rovnakým smerom. Počas nasledujúceho časového intervalu, ktorý sa rovná prvému, prebehne Achilles ďalších tisíc krokov a korytnačka prejde sto krokov. Teraz je Achilles osemsto krokov pred korytnačkou.

Tento prístup adekvátne popisuje realitu bez akýchkoľvek logických paradoxov. Ale to nie je úplné riešenie problému. Einsteinov výrok o neprekonateľnosti rýchlosti svetla je veľmi podobný Zenónovej apórii „Achilles a korytnačka“. Tento problém musíme ešte študovať, prehodnotiť a vyriešiť. A riešenie treba hľadať nie v nekonečne veľkých číslach, ale v merných jednotkách.

Ďalšia zaujímavá aporia Zeno hovorí o lietajúcom šípe:

Letiaci šíp je nehybný, pretože v každom okamihu je v pokoji, a keďže je v každom okamihu v pokoji, je vždy v pokoji.

V tejto apórii je logický paradox prekonaný veľmi jednoducho - stačí objasniť, že letiaci šíp v každom okamihu spočíva na rôznych bodoch priestoru, čo je v skutočnosti pohyb. Tu je potrebné poznamenať ešte jeden bod. Z jednej fotografie auta na ceste nie je možné určiť ani skutočnosť jeho pohybu, ani vzdialenosť k nemu. Na určenie skutočnosti pohybu auta sú potrebné dve fotografie nasnímané z toho istého bodu v rôznych časových okamihoch, ale nemožno ich použiť na určenie vzdialenosti. Na určenie vzdialenosti od auta potrebujete dve fotografie nasnímané z rôznych bodov v priestore súčasne, ale nemôžete z nich určiť skutočnosť pohybu (prirodzene stále potrebujete ďalšie údaje na výpočty, pomôže vám trigonometria). Chcem poukázať najmä na to, že dva body v čase a dva body v priestore sú dve rôzne veci, ktoré by sa nemali zamieňať, pretože poskytujú rôzne príležitosti na prieskum.
Postup ukážem na príklade. Vyberáme "červenú tuhú látku v pupienku" - to je náš "celok". Zároveň vidíme, že tieto veci sú s mašľou a sú bez mašle. Potom z "celku" vyberieme časť a zostavíme "s mašličkou". Takto sa šamani živia spájaním svojej teórie množín s realitou.

Teraz urobme malý trik. Zoberme si "pevné v pupienke s lukom" a zjednoťme tieto "celé" podľa farby, pričom vyberieme červené prvky. Dostali sme veľa „červenej“. Teraz záludná otázka: sú prijaté súpravy „s mašľou“ a „červenou“ tou istou súpravou alebo dvoma rôznymi súpravami? Odpoveď poznajú len šamani. Presnejšie, oni sami nič nevedia, ale ako sa hovorí, tak je.

Tento jednoduchý príklad ukazuje, že teória množín je úplne zbytočná, pokiaľ ide o realitu. Aké je to tajomstvo? Vytvorili sme sadu "červený pevný pupienok s mašľou". Formovanie prebiehalo podľa štyroch rôznych merných jednotiek: farba (červená), sila (plná), drsnosť (v hrboľke), ozdoby (s mašličkou). Iba súbor meracích jednotiek umožňuje adekvátne opísať skutočné objekty v jazyku matematiky. Takto to vyzerá.

Písmeno "a" s rôznymi indexmi označuje rôzne jednotky merania. V zátvorkách sú zvýraznené merné jednotky, podľa ktorých je „celok“ priradený v prípravnom štádiu. Jednotka merania, podľa ktorej je zostava vytvorená, sa vyberie zo zátvoriek. Posledný riadok zobrazuje konečný výsledok - prvok sady. Ako vidíte, ak použijeme jednotky na vytvorenie množiny, potom výsledok nezávisí od poradia našich akcií. A toto je matematika a nie tance šamanov s tamburínami. Šamani môžu „intuitívne“ dospieť k rovnakému výsledku, argumentujúc „samozrejmosťou“, pretože merné jednotky nie sú zahrnuté v ich „vedeckom“ arzenáli.

Pomocou meracích jednotiek je veľmi jednoduché rozbiť jednu alebo spojiť niekoľko sád do jednej nadmnožiny. Pozrime sa bližšie na algebru tohto procesu.

Pamätajte!

Pri troch známych členoch podielu môžete vždy nájsť jeho neznámeho (štvrtého) člena.

vyriešiť pomer znamená nájsť všetkých jej členov. Vyriešme pomer nižšie
(nájdite "x").

Na nájdenie "x" používame hlavnú vlastnosť proporcie (pravidlo "kríž").

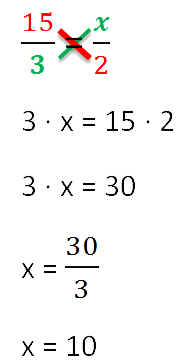
Teraz sme pripravení zistiť, ako vyriešiť proporčné problémy.

Riešenie problémov s proporciami

Často pomerné úlohyúzko súvisí s percentami. Svoje znalosti o percentách si môžete oprášiť v sekcii „Záujmy“.

Úloha

Z luku bolo vypálených 50 rán. Okolo cieľa preletelo 5 šípov. Určite percento zásahov.

Podľa tradície kladieme v úlohe dôraz na dôležité a číselné údaje.

Upozorňujeme, že musíme určiť percento zásahov, nie percento vynechaných šípov.

Preto najprv vypočítame, koľko šípov zasiahne cieľ. Nebude ťažké to urobiť.

50 − 5 = 45 (šípky) – zasiahnite cieľ.

Ďalej, aby sme problém vyriešili, urobíme tabuľku, do ktorej zadáme všetky údaje. Pamätajte, že oproti 100% v tabuľke je zvyčajne napísané celkové množstvo niečoho. Neznáme percentá budú označené písmenom x.

Aby ste správne zaznamenali potrebné údaje do tabuľky, nezabudnite na jednoduché pravidlo.

Rovnosť dvoch pomerov sa nazýva pomer.

a :b =c :d. Toto je pomer. Čítať: A tak platí pre b, Ako c odkazuje na d. čísla a A d volal extrémnačlenov podielu a čísla b A c – priemerčlenov podielu.

Príklad proporcie: 1 2 : 3 = 16 : 4 . Toto je rovnosť dvoch pomerov: 12:3= 4 a 16:4= 4 . Čítajú: dvanásť je na tri ako šestnásť na štyri. Tu sú 12 a 4 krajné členy podielu a 3 a 16 sú stredné členy podielu.

Základná vlastnosť proporcie.

Súčin extrémnych členov podielu sa rovná súčinu jeho stredných členov.

Pre proporcie a :b =c :d alebo a/b=c/d hlavná vlastnosť je napísaná takto: a d \u003d b c .

Pre náš pomer 12 : 3 = 16 : 4 bude hlavná vlastnosť napísaná takto: 12 4 = 3 16 . Ukazuje sa správna rovnosť: 48 \u003d 48 .

Ak chcete nájsť neznámy extrémny člen podielu, musíte rozdeliť súčin priemerných členov podielu známym extrémnym členom.

Príklady.

1) x : 20 = 2 : 5. Máme X A 5 sú krajnými členmi podielu a 20 A 2 - stredný.

Riešenie.

x = (202):5- musíte vynásobiť stredné členy ( 20 A 2 ) a výsledok vydeľte známym extrémnym členom (číslo 5 );

x = 40:5 je súčinom stredných členov ( 40 ) deliť známym extrémnym pojmom ( 5 );

x = 8. Dostali sme požadovaný extrémny termín podielu.

Výhodnejšie je zapísať nález neznámeho člena podielu pomocou obyčajného zlomku. Príklad, ktorý sme uvažovali, by potom bol napísaný takto:

Požadovaný extrémny termín podielu ( X) sa bude rovnať súčinu stredných členov ( 20 A 2 ) delené známym extrémnym pojmom ( 5 ).

Zlomok znížime o 5 (rozdeliť podľa 5 X.

Viac takýchto príkladov nájdenia neznámeho krajného člena proporcie.

Ak chcete nájsť neznámy stredný člen podielu, musíte rozdeliť súčin extrémnych členov podielu známym stredným členom.

Príklady. Nájdite neznámy stredný člen podielu.

5) 9 : x = 3 : 14.číslo 3 je známy priemerný člen daného podielu, čísla 9 A 14 sú extrémne pomery.

Riešenie.

x \u003d (9 14): 3 - vynásobte krajné členy podielu a výsledok vydeľte známym stredným členom podielu;

x = 136:3;

x=42.

Riešenie tohto príkladu môže byť napísané inak:

Požadované priemerné trvanie podielu ( X) sa bude rovnať súčinu extrémnych výrazov ( 9 A 14 ) delené známym stredným členom ( 3 ).

Zlomok znížime o 3 (rozdeliť podľa 3 a čitateľ a menovateľ zlomku). Nájdenie hodnoty X.

Ak ste zabudli, ako znížiť bežné zlomky, zopakujte tému: ""

Viac takýchto príkladov na nájdenie neznámeho priemerného člena podielu.

Sekcie: Matematika

Typ vyučovacej hodiny: Hodina štúdia a primárneho upevňovania nových vedomostí.

Forma lekcie: Lekcia-výskum.

Ciele lekcie:

aktivovať kognitívnu činnosť žiakov;
oboznámiť žiakov s pojmami: proporcia, členovia proporcie; správne a nesprávne proporcie;
oboznámiť žiakov so základnou vlastnosťou proporcie a formovať zručnosť určovať správnu proporciu.

Vybavenie:

Hárky trás označujú body, ktoré je možné získať za riešenie úloh. Žiak pri bodovaní prihliada na správnosť svojho rozhodnutia, rýchlosť rozhodnutia (samokontrola a vzájomná kontrola pomocou prezentácie). V riadku „Dodatočné body“ sú body uvedené za zodpovedanie dodatočných otázok, za pomoc učiteľovi pri organizovaní testovania ostatných študentov a tiež za „uhádnutie“ témy hodiny.

Karty sa rozrežú a rozdajú študentom v obálkach (jedna obálka na stôl).

3. Karty pre magnetickú tabuľu (obrázok 1, obrázok 2, obrázok 3)

Počas hodiny sú tieto kartičky vyvesené na magnetickej tabuli.

4. Hádanky (Obrázok 4, Obrázok 5, Obrázok 6, Obrázok 7).

Rébusy zostavené stredoškolákmi (okrem rébusu „Proporcia“ - tento rébus bol prevzatý z hodiny prezentovanej na FPI učiteľkou Kozákom Tatyanou Ivanovnou, stredná škola č. 20 Pokrok, Amurský kraj) sú umiestnené na tabuli, študenti sú vyzvaní, aby ich vyriešili po lekcii.

Technickým vybavením hodiny je počítač, projektor na ukážku prezentácie, plátno. Počítačová prezentácia v programe Microsoft PowerPoint (príloha 4).

I. Organizácia začiatku vyučovacej hodiny

Ahoj! Skontrolujte si, prosím, či máte na stole písomky, či máte červenú a modrú ceruzku a či ste pripravení na hodinu.

II. Témy správ, ciele a ciele lekcie.

Dnes na lekcii pokračujeme v štúdiu veľkej časti kurzu matematiky. Dokončili sme štúdium témy (čo? - "postoj"). Teraz začíname skúmať novú tému v tejto časti. Niekoľko príkladov nám pomôže pochopiť tému lekcie. Na titulnej strane vášho trasového listu je potrebné vyplniť tabuľku ústnym vyriešením príkladov a potom budete poznať tému dnešnej hodiny. ŠMYKĽAVKA 1

Takže téma dnešnej lekcie Proporcia. SNÍMKA 2

Keď poznáte tému lekcie, skúste si zostaviť plán lekcie. Čo by ste sa mali dnes na hodine naučiť? Čo chceš vedieť? Čo sa chceš na hodine naučiť?

Urobíme si plán, ktorý budeme počas hodiny dopĺňať. (študenti vymenujú prvé dva a posledné dva body plánu, ostatné vypĺňajú počas hodiny, keď sa „objavujú“ nové poznatky; plán hodiny je napísaný na tabuli)

- opakovanie (otázky súvisiace s postojom)

Definícia proporcie

PROPORCENTNÍ ČLENOVIA

SPRÁVNE A NESPRÁVNE PROporcie

HLAVNÉ VLASTNOSTI PROPORCIE

Aplikácia v matematike

Aplikácia v živote

Posledné dva body budeme môcť analyzovať v nasledujúcich lekciách pri štúdiu témy.

III. Aktualizácia vedomostí žiakov. Príprava na aktívnu vzdelávaciu a kognitívnu činnosť v hlavnej fáze hodiny.

Diskutujte o otázkach týkajúcich sa témy „Postoj“ so spolužiakom.

Kto je pripravený klásť otázky týkajúce sa poslednej témy? (blizzard) MP1

- Čo je to postoj?

Ako môžete napísať vzťah?

Na aké otázky odpovedá postoj?

Ako môžete napísať pomer dvoch čísel?

Čo môže nahradiť znak robiť?

Prečo si myslíte, že sme tieto pojmy zopakovali?

Pomôžu nám pri učení novej témy.

Vezmite obálky a vytvorte vzťah A Komu b A c Komu d dve cesty. (iba 4 vzťahy) PRACUJTE VO DVOCH.

MP2 Máte pred sebou niekoľko vzťahov. Nájdite význam týchto výrazov. ŠMYKĽAVKA 3

4: 0,5=
=
5: 10 =
=
8: 1 =
2,5: 5 =

Zoskupte vzťahy podľa určitého atribútu a vytvorte zodpovedajúce rovnosti.

IV. Asimilácia nových poznatkov.

4: 0,5 = 8: 1 = 5: 10 = 2,5: 5

Na základe čoho ste zoskupili tieto vzťahy?

- Ich hodnoty sú rovnaké.

Výsledné rovnosti sa nazývajú proporcie.

Premýšľajte a definujte pomer.

TIP – pomer je ... NA OBRAZOVKE ( rovnosť)

Rovnosť ...ČOHO ( vzťahy)

Koľko vzťahov? ( dva).

Kto si je istý svojim názorom, zapíše definíciu do hárku trasy. MP3

Kto je pripravený ísť k tabuli a zostaviť definíciu proporcie? (príloha 3)

DEFINÍCIA (na magnetickej tabuli): Proporcia je rovnosť dvoch pomerov.

Pozrime sa na výklad slova proporcia v slovníku ruského jazyka Ozhegov S.I. ŠMYKĽAVKA 4: „Proporcia je určitý pomer častí k sebe, proporcionalita. V matematike rovnosť dvoch pomerov.

Definíciu proporcie ste sformulovali aj v slovníku ruského jazyka!

Zamyslite sa nad tým, s akým matematickým výrazom sa zhoduje slovo „proporcia“? ( záujem). Ako sa prekladá výraz „percento“? ( od stovky). Takže „pro“ sa prekladá ako „od“. Aká časť slova zostala? (“ porcia“). Kde ste na toto slovo natrafili? (pri varení)Čo to znamená? ( veľkosť)

Slovo proporcia pochádza z latinského slova proportio – proporcionalita. (etymologický slovník). ŠMYKĽAVKA 4

Pomocou definície proporcie napíšte proporcie pomocou znamienka delenia a zlomkovej čiary. (PRÁCA VO DVOCH, obálky).

V hárkoch trasy zapíšte pomer pomocou písmen a B C d. MP4

A teraz zistíme, ako sa nazývajú čísla, ktoré tvoria podiel.

čísla a B C d zvaných členov podielu

Aký je prvý a posledný člen podielu? ( a a c)

A čo sa zvyčajne (v živote) nazýva prvé a posledné? (extrémne)

Takže výrazy a a b sa nazývajú ...? (extrémne)

Kde sú výrazy c a d? (v strede)

A ako sa volajú členovia c a d? ( stredný)

Ktorí členovia sú zvýraznení červenou farbou? ( Komu skoro)

farba (s zriedkavé)členov.

strední členovia

Vráťme sa k plánu hodiny – máte k nemu niečo doplniť? (krajné a stredné členy podielu)

V. Primárne upevnenie vedomostí

MP5 Vyplňte tabuľku:

Aký záver možno vyvodiť? Zaznamenajte výstup do itinerára. ( V pomere sa súčin extrémnych členov rovná súčinu stredných členov)ŠMYKĽAVKA 8

MP6 Tu je päť rovností. Sú to všetky proporcie?

Zdôraznite proporcie.

= ; 7 + 11 = 36: 2; 72: 9 = 16: 2; = 20: 4; 5 40 = 100 2

SNÍMKA 7 Postavte sa, kto skončil.

Je si každý istý, že sú tu tri proporcie? V poslednej rovnosti sa totiž súčin extrémnych pojmov nerovná súčinu stredných. Vráťme sa k definícii proporcie ( Proporcia - rovnosť dvoch pomerov). Je tretia rovnosť rovnosťou dvoch vzťahov? (je). Podľa definície, je to pomer? (Áno). Rovná sa súčin extrémnych výrazov súčinu stredných výrazov? (nie). Takže je to pomer...? (nesprávne). Tento podiel sa nazýva nesprávny. Takže existujú nesprávne proporcie a ...? (verný). Formulujte hlavnú vlastnosť podielu pomocou získaných vedomostí. (V správnom pomere sa súčin extrémnych členov rovná súčinu stredných).

VI. Upevnenie vedomostí.

Vyplňte tabuľku.

Správny pomer Nesprávny pomer

= = 20: 4

Ako inak môžete určiť správny alebo nesprávny pomer? (nájdi hodnotu vzťahu)

V budúcnosti si povieme o správnych proporciách.

Vráťme sa k plánu lekcií. Čo možno pridať? (správne a nesprávne proporcie)

MP7 Pomocou písmen B a H označte správne a nesprávne proporcie.

= 1: 0,5 = 4,8: 2,4
7,5: 5 = 2: 3 =
10: 3 = 3 : 1 5:x = 20:4x

VII. Zovšeobecňovanie a systematizácia.

MP8 Pomocou základnej vlastnosti proporcie zostavte správny pomer z nasledujúcich čísel: 4, 5, 12, 15. Koľko správnych pomerov dokážete?

VIII. Kontrola a autotest vedomostí

MP9 matematický diktát

Zapíšte pomer: Číslo 18 súvisí so 4, zatiaľ čo 27 súvisí so 6.
Napíšte pomer: Pomer tri ku piatim sa rovná pomeru dva ku siedmim.
Zapíšte si priemerné pomery: 1,5: 2 \u003d 4,5: 6
Zapíšte krajné členy podielu: 2/1,9 = 3/2,8
Je pomer v odseku 3 správny?
Je pomer v položke 4 správny?
Je tvrdenie pravdivé: Koreň rovnice je 20/5 \u003d x / 0,5 číslo 2
Platí nasledujúce tvrdenie: Akékoľvek štyri prirodzené čísla možno použiť na vytvorenie podielu?

ŠMYKĽAVKA 10. Odborné hodnotenie

IX. Zhrnutie lekcie.

Pozrite si plán lekcie.

Čo ste sa dnes v triede naučili? (čo je proporcia, z čoho pozostáva proporcia, proporcie sú pravdivé a nesprávne, hlavná vlastnosť pomeru, ...)

Čo ste sa dnes v triede naučili? (určte krajný a stredný člen podielu, zistite, či je pomer správny alebo nesprávny, ...)

Aké ďalšie otázky možno položiť na konci lekcie?

-Koľko správnych proporcií možno urobiť z tohto správneho pomeru?

Ako zistíte, či je pomer správny alebo nesprávny?

Spomeňme si na poslednú úlohu matematického diktátu.

Na vytvorenie proporcie možno použiť akékoľvek štyri prirodzené čísla. Správna odpoveď je ÁNO. Môžete nakresliť pomer, ale nemusí to byť nevyhnutne pravda.

Z frázy " Na vytvorenie proporcie možno použiť akékoľvek štyri prirodzené čísla. Odstráňte jedno slovo, aby bolo toto tvrdenie nesprávne. (prirodzený). prečo? (Číslo 0 nemôže byť členom proporcie). Na vytvorenie proporcie možno použiť ľubovoľné štyri čísla

V tejto fráze Na vytvorenie proporcie možno použiť akékoľvek štyri prirodzené čísla. vložte jedno slovo, aby bol výrok nesprávny (pravda). Z ľubovoľných štyroch prirodzených čísel môžete urobiť správny pomer.

Vypočítajte počet bodov, ktoré ste na lekcii získali, a priraďte im známku.

X. Informácie o domácej úlohe a návod na jej vyplnenie

Matematika - 6, Vilenkin N.Ya. a kol., 6. vydanie

S.21, č. 760, 781, 782, 783 (a)

Pomer dvoch čísel

Definícia 1

Pomer dvoch čísel je ich súkromný.

Príklad 1

pomer 18 $ ku 3 $ možno zapísať ako:

$18\div 3=\frac(18)(3)=6$.

pomer $ 5 $ k $ 15 $ možno zapísať ako:

$5\div 15=\frac(5)(15)=\frac(1)(3)$.

Používaním pomer dvoch čísel možno ukázať:

koľkokrát je jedno číslo väčšie ako druhé;
akú časť predstavuje jedno číslo od druhého.

Pri zostavovaní pomeru dvoch čísel v menovateli zlomku zapíšte číslo, s ktorým sa porovnáva.

Najčastejšie takéto číslo nasleduje za slovami „v porovnaní s ...“ alebo pred predložkou „k ...“.

Pripomeňte si základnú vlastnosť zlomku a aplikujte ju na vzťah:

Poznámka 1

Pri vynásobení alebo delení oboch členov vzťahu rovnakým číslom iným ako nula dostaneme pomer, ktorý sa rovná pôvodnému.

Uvažujme o príklade, ktorý ilustruje použitie konceptu pomeru dvoch čísel.

Príklad 2

Množstvo zrážok v predchádzajúcom mesiaci bolo 195 USD mm a v aktuálnom mesiaci - 780 USD mm. O koľko sa zvýšil úhrn zrážok v aktuálnom mesiaci v porovnaní s predchádzajúcim mesiacom?

Riešenie.

Zostavte pomer množstva zrážok v aktuálnom mesiaci k množstvu zrážok v predchádzajúcom mesiaci:

$\frac(780)(195)=\frac(780\div 5)(195\div 5)=\frac(156\div 3)(39\div 3)=\frac(52)(13)=4 $.

Odpoveď: množstvo zrážok v aktuálnom mesiaci je 4 $ krát viac ako v predchádzajúcom mesiaci.

Príklad 3

Zistite, koľkokrát je číslo $1 \frac(1)(2)$ obsiahnuté v čísle $13 \frac(1)(2)$.

Riešenie.

$13 \frac(1)(2)\div 1 \frac(1)(2)=\frac(27)(2)\div \frac(3)(2)=\frac(27)(2) \cdot \frac(2)(3)=\frac(27)(3)=9$.

Odpoveď: 9 $ krát.

Pojem proporcie

Definícia 2

Proporcia sa nazýva rovnosť dvoch vzťahov:

$a\div b=c\div d$

$\frac(a)(b)=\frac(c)(d)$.

Príklad 4

$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,

$\frac(8)(2)=\frac(36)(9)$, $\frac(10)(40)=\frac(9)(36)$, $\frac(15)(75)= \frac(1)(5)$.

V pomere $\frac(a)(b)=\frac(c)(d)$ (alebo $a:b = c\div d$) sa čísla a a d nazývajú extrémnych členov proporcie, kým čísla $b$ a $c$ sú strední členovia proporcie.

Správny pomer je možné previesť takto:

Poznámka 2

Súčin extrémnych členov správneho podielu sa rovná súčinu stredných členov:

$a \cdot d=b \cdot c$.

Toto vyhlásenie je základná vlastnosť proporcie.

Opak je tiež pravdou:

Poznámka 3

Ak sa súčin extrémnych členov podielu rovná súčinu jeho stredných členov, potom je podiel správny.

Poznámka 4

Ak sú stredné výrazy alebo extrémne výrazy usporiadané v správnom pomere, potom budú správne aj získané proporcie.

Príklad 5

$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,

$\frac(2)(8)=\frac(9)(36)$, $\frac(40)(10)=\frac(36)(9)$, $\frac(75)(15)= \frac(5)(1)$.

Pomocou tejto vlastnosti je ľahké nájsť neznámy výraz z podielu, ak sú známe ďalšie tri:

$a=\frac(b \cdot c)(d)$; $b=\frac(a \cdot d)(c)$; $c=\frac(a \cdot d)(b)$; $d=\frac(b \cdot c)(a)$.

Príklad 6

$\frac(6)(a)=\frac(16)(8)$;

$6 \cdot 8=16 \cdot a$;

$16 \cdot a=6 \cdot 8$;

$16 \cdot a=48$;

$a=\frac(48)(16)$;

Príklad 7

$\frac(a)(21)=\frac(8)(24)$;

$a \cdot 24=21 \cdot 8$;

$a \cdot 24=168$;

$a=\frac(168)(24)$;

3 doláre záhradník - 108 dolárov stromy;

$x$ záhradníci - $252$ strom.

Urobme pomer:

$\frac(3)(x)=\frac(108)(252)$.

Použime pravidlo na nájdenie neznámeho členu podielu:

$b=\frac(a \cdot d)(c)$;

$x=\frac(3 \cdot 252)(108)$;

$x=\frac(252)(36)$;

Odpoveď: Orezať stromy v hodnote 252 $ bude trvať záhradkárom 7 $.

Najčastejšie sa vlastnosti proporcie používajú v praxi pri matematických výpočtoch v prípadoch, keď je potrebné vypočítať hodnotu neznámeho člena proporcie, ak sú známe hodnoty ostatných troch členov.